Aqui daremos início ao estudo dos fenômenos térmicos, sabendo que são aqueles que estão relacionados às variações de temperatura. Compreenderemos a definição de temperatura, qual a sua relação com o movimento das moléculas de um corpo e como é feita a sua medida. Exploraremos os diferentes tipos de termômetros e seus modos de funcionamento.
Como a temperatura pode ser medida em diversas escalas, faremos um estudo das escalas termométricas mais utilizadas mundialmente, Celsius, Fahrenheit e Kelvin e estabeleceremos uma relação matemática entre elas para efetuarmos a conversão de temperatura. Praticaremos a medida de variação de temperatura e descobriremos como converter uma variação de temperatura de uma escala para a outra.
Estabeleceremos definições cuidadosas não só para a temperatura, mas para a energia térmica e o calor, para facilitar uma descrição quantitativa dos fenômenos térmicos. Definiremos o conceito de calor, estabelecermos os mecanismos pelos quais o calor pode fluir e aprenderemos a calcular as quantidades de calor latente e calor sensível.
Estudaremos como a variação de temperatura pode alterar as dimensões de um corpo, resultando em dilatação ou contração do mesmo. Abordaremos três tipos de expansão, a dilatação linear, superficial e volumétrica. Por fim, veremos como ocorre a expansão térmica de um gás ideal, confinado em um cilindro com êmbolo móvel e mantido à pressão constante
Em sua leitura, atente-se à definição do conceito de temperatura, que costuma ser confundida com o calor, devido a uma questão linguística e um erro conceitual. Embora o senso comum utilize o termo “quente” para se referir a uma alta temperatura e o termo “frio” para se referir a uma baixa temperatura, temperatura e calor não são sinônimos. A temperatura está relacionada à agitação dos átomos, ou moléculas, que compõem o corpo.
Ao adentrar no estudo do calor, foque sua atenção na definição de seu conceito e na diferença entre os conceitos de calor e energia térmica. Dê atenção aos mecanismos pelos quais o calor flui e, principalmente, atente-se às duas diferentes situações às quais um corpo está sujeito ao receber ou ceder calor, ou passará por uma mudança em sua temperatura ou passará por uma mudança de estado físico. Observe que essas mudanças nunca ocorrerão simultaneamente, ou o corpo está mudando de fase ou de temeperatura.
Por fim, atente-se ao efeito da mudança de temperatura em sólidos, líquidos e gases, essa alteração da temperatura provocará um aumento nas dimensões do corpo, chamada de dilatação. Cada substância sofrerá, para uma mesma variação de temperatura, uma dilatação diferente, que dependerá do calor específico da substância.
Nos temas a seguir, você irá aprofundar seu conhecimento com o estudo dos assuntos específicos desta unidade e, ao final, deverá atingir os seguintes objetivos de aprendizagem:
- Identificar o conceito de temperatura.
- Diferenciar as escalas termométricas.
- Calcular a quantidade de calor sensível e latente.
- Interpretar uma curva de aquecimento.
- Calcular os diferentes tipos de dilatação.
Tema 1 - Termologia - Conceitos Fundamentais
Neste tema, abordaremos o conceito de temperatura, que é uma propriedade de um sistema macroscópico. Sistemas macroscópicos são formados por um grande número de moléculas e possuem dimensões que nos permite vê-los a olho nu ou tocá-los.
Exemplos cotidianos de sistemas macroscópicos podem ser um recipiente com água, um balão cheio de gás, ou ainda, um iceberg. Chamamos de propriedades macroscópicas àquelas propriedades que, como:
- • a massa;
- • a pressão;
- • a temperatura;
- • a densidade;
- • o volume.
Todas essas caracterizam um sistema macroscópico.
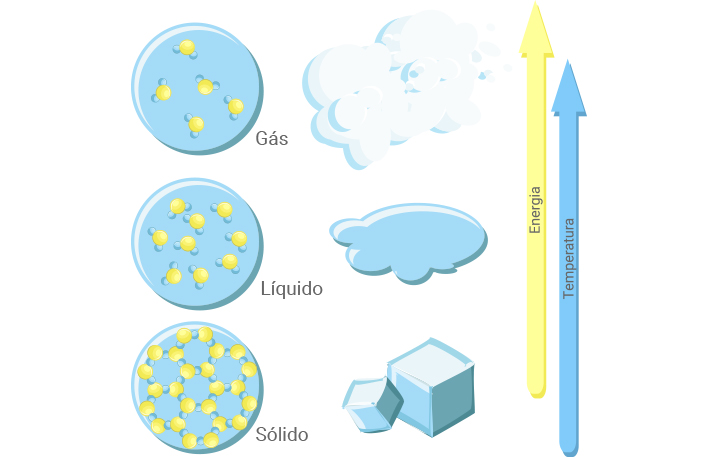
Figura 1 : Propriedades macroscópicas. Fonte: Dreamstime.
Analisaremos a temperatura, como pode ser definida, como pode ser medida e como ela pode afetar os corpos. Como a temperatura caracteriza um sistema macroscópico, teremos neste tema um objetivo duplo, compreender essa propriedade e relacioná-la ao movimento das moléculas subjacentes, que representam um sistema microscópico.
Em termos mais simples, desenvolveremos uma conexão micro/macro, buscando compreender uma propriedade macroscópica dos sólidos, líquidos e gases em função do movimento de suas moléculas. Por fim, estudaremos os dispositivos que medem a temperatura e as diferentes escalas que a quantificam.
Temperatura
O termo “temperatura” não é uma novidade para nós, provavelmente o utilizamos diariamente em nosso cotidiano para descrever o quão “quente” ou “frio” um corpo está. Ouvimos na previsão do tempo que o dia de hoje terá a temperatura mínima de 23°C e a máxima de 30°C.
Aprendemos que se o corpo humano estiver com temperatura a partir de 37°C trata-se de uma febre.
Mas o que exatamente a temperatura mede?
Sabemos que a massa de um corpo mede, basicamente, a quantidade de matéria e que a velocidade mede a rapidez com que o corpo se movimenta.
Mas e a temperatura?
Apenas a princípio, partiremos da ideia que vem do senso comum de que a temperatura diz se um corpo está “quente” ou “frio” e utilizaremos esses termos apenas como um fim didático para atingir o conceito de temperatura.
Se pudéssemos enxergar as moléculas dos corpos, como na Figura 2, veríamos que as moléculas do corpo “quente” estão muito mais agitadas que as moléculas do corpo “frio”, o que nos leva a conclusão de que a temperatura se relaciona com o grau de agitação das moléculas.
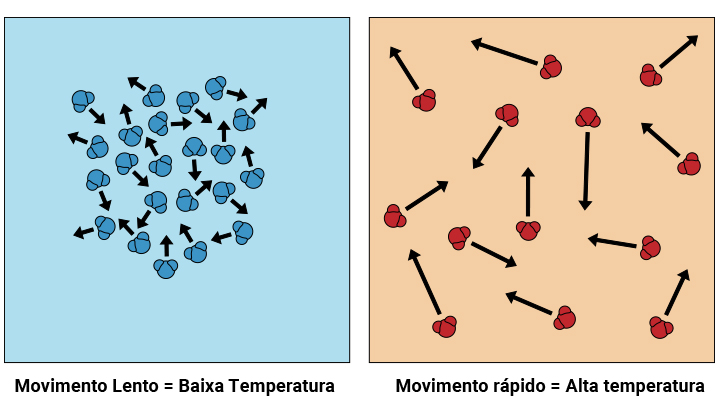
Figura 2 : Movimento das moléculas de um corpo com diferentes temperaturas. Fonte:
Dreamstime.
Aprofundaremos ainda mais o conceito de temperatura na Unidade de Aprendizagem 4, que trata da termodinâmica, e estabeleceremos uma relação precisa entre temperatura e energia térmica. Mas, já temos um conceito definido aqui para a temperatura: temperatura é a medida do grau de agitação das moléculas.
Para medir a temperatura de um corpo, necessitamos de um aparelho chamado termômetro. Os termômetros utilizam como base uma substância que tenha alguma propriedade que se altera com a mudança de temperatura.
São exemplos de propriedades que variam com a temperatura:
- o volume de um líquido;
- a pressão em um gás mantido em volume constante;
- o comprimento de um sólido;
- a resistência elétrica de um fio condutor;
- até mesmo a cor de um corpo.
Os termômetros de uso doméstico, em geral, utilizam em seu interior uma coluna de líquido, mercúrio ou álcool, que fica livre para expandir dentro de um tubo capilar de vidro.
Nesse caso, o volume do líquido é a propriedade que varia de acordo com a temperatura, ou seja, se a temperatura aumentar ou diminuir, a coluna de mercúrio aumentará ou diminuirá proporcionalmente, como mostra a Figura 3.

Figura 3: Termômetro antes e depois do contato com água quente. Fonte: Jewett Jr.;
Serwat (2013, p. 144).
O termômetro deve ser colocado em contato com o sistema cuja temperatura deseja-se medir e, no caso de um termômetro de álcool ou mercúrio, o pequeno volume dessas substâncias irá se expandir ou se contrair de acordo com a temperatura do objeto de contato.
Existem outros tipos de termômetros, por exemplo:
O termômetro a gás, dentre os termômetros científicos, é um dos mais importantes, pois é o que mais se aproxima de um termômetro universal, ou seja, suas leituras serão independes da substância utilizada nele.
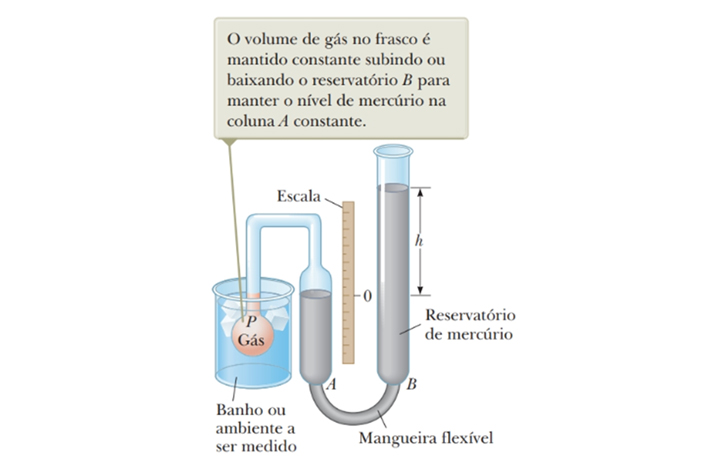
Figura 4: Termômetro a gás. Fonte: Jewett Jr.; Serwat (2013, p. 115).
Para calibrar um termômetro de gás, é necessário, antes de mais nada, registrar a pressão do gás para duas temperaturas de referência, geralmente, os pontos de ebulição e solidificação da água.
De posse desses pontos, é possível plotar o gráfico de pressão versus temperatura, e como a relação entre essas grandezas é linear, uma linha reta é traçada entre essas temperaturas de referência, como ilustra a Figura 5.
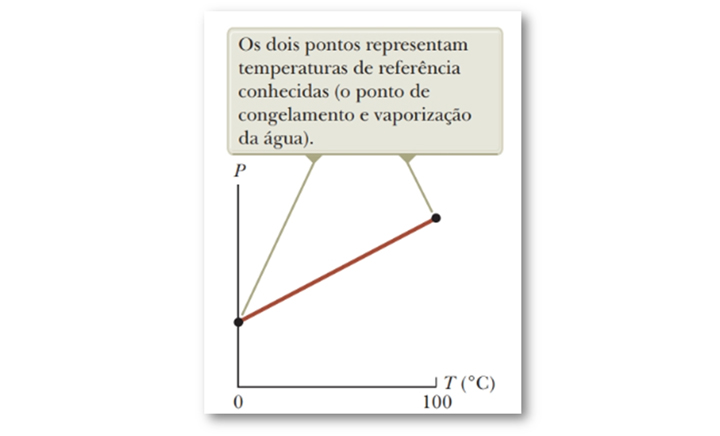
Figura 5: Gráfico de pressão versus temperatura obtido por um termômetro de gás
com
volume constante. Fonte: Jewett Jr.; Serwat (2013, p. 115).
Por fim, é necessário colocar o reservatório do gás em contato com o sistema para o qual desejamos aferir a temperatura, assim, mede-se a pressão e busca-se no gráfico a temperatura correspondente.
Podemos observar, na Figura 6, um gráfico de pressão versus temperatura, obtido por meio de termômetros que utilizam três gases distintos.
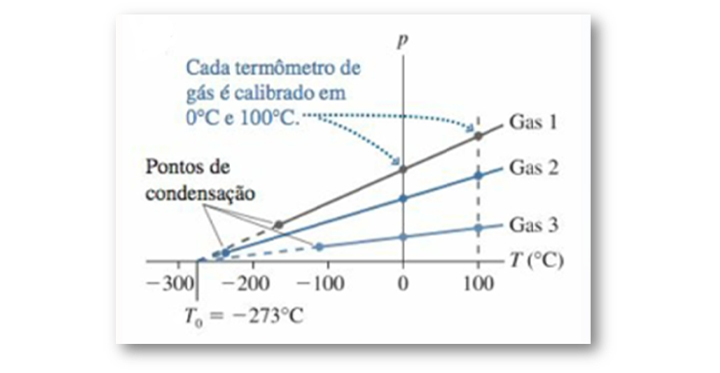
Figura 6: Gráfico de pressão versus temperatura de três gases distintos. Fonte:
Knight
(2009, p. 67).
Devemos destacar duas informações muito relevantes obtidas a partir da análise desse gráfico: a primeira é que a temperatura e a pressão variam de modo proporcional, ou seja, a relação entre pressão e temperatura é linear; a segunda é que todos os gases terão a pressão tendendo a zero para a mesma temperatura, -273°C.
Curiosidade
A menor temperatura que podemos registrar utilizando o termômetro de gás é de, aproximadamente, 1 K. Para atingir essa temperatura tão baixa é preciso utilizar gás hélio a baixa pressão, pois este gás, mais do que qualquer outro, permanece no estado gasoso mesmo para temperaturas muito baixas.
Essa última análise mostra uma importante atribuição dessa temperatura específica, ela é usada como a base para a escala de temperatura absoluta, ou escala Kelvin, que estabelece –273,15 °C (ou –273, de forma aproximada) como seu ponto zero.
Escalas Termométricas
Um possível método para calibrar um termômetro consiste em colocá-lo em contato com um sistema natural que permaneça em temperatura constante, como uma mistura de água com gelo, ambos já a mesma temperatura (equilíbrio térmico), à pressão atmosférica.
A temperatura dessa mistura é chamada de ponto de solidificação, ou ponto de congelamento, da água. A mistura de água com vapor d’água em equilíbrio térmico, à pressão atmosférica, também é utilizada como parâmetro, e a temperatura dessa mistura é conhecida como ponto de ebulição, ou ponto de vaporização, da água.
Diversos sistemas já foram utilizados para quantificar temperatura e com isso diversas escalas termométricas surgiram, entretanto, as Celsius, Fahrenheit e Kelvin são as mais utilizadas.
Por conta das cem partes iguais, a escala Celsius também é conhecida como escala centígrada.
A unidade de temperatura do SI é o Kelvin, e não se diz grau Kelvin.
A Figura 7 resume os pontos de solidificação, ebulição e zero absoluto nas escalas Celsius, Fahrenheit e Kelvin.

Figura 7: Relação entre temperaturas nas escalas Kelvin, Celsius e Fahrenheit. Fonte:
Dreamstime.
Como existem diversas escalas termométricas, não são raras as vezes em que é necessário transformar a indicação numérica de uma escala para outra.
Se medíssemos a temperatura de um corpo com três termômetros de mercúrio diferentes, graduados em Celsius, Fahrenheit e Kelvin, obteríamos os seguintes seguimentos de mercúrio (Figura 8), que independem da escala em que foram obtidos.
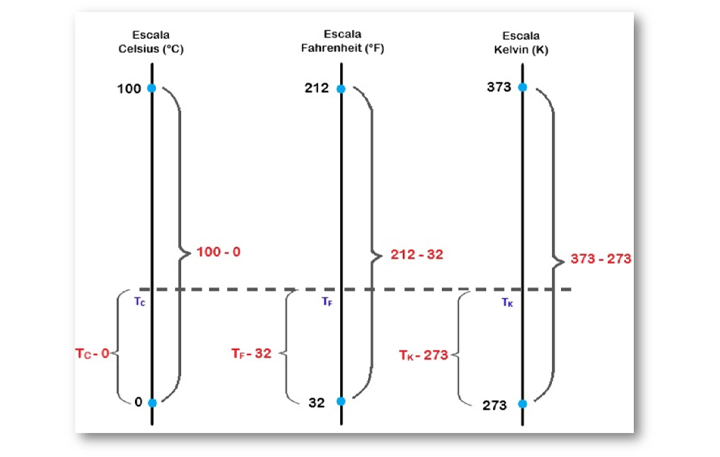
Figura 8 : Relação entre as escalas termométricas. Fonte: Elaborada pela autora.
Logo, chegamos à seguinte relação matemática entre as escalas Celsius, Fahrenheit e Kelvin.
Ou, ainda, de forma simplificada:
Uma simples relação entre as escalas Celsius e Kelvin é dada por:
Vejamos alguns exemplos de aplicação dessas equações.
1. Durante uma viagem de férias aos Estados Unidos, um brasileiro teve um mal-estar e, suspeitando estar com febre, aferiu sua temperatura corporal utilizando um termômetro graduado em Fahrenheit.
O termômetro registrou a temperatura de 100,4°F e o turista converteu para Celsius para saber se estava ou não com febre.
Qual foi o valor encontrado na escala Celsius?
Ele estava realmente com febre?
Vamos utilizar a relação entre as escalas de interesse, Celsius e Fahrenheit:
Substituindo o valor da temperatura em Fahrenheit, temos:
A temperatura dele em Celsius era 38°C, que significa que ele realmente estava com febre.
2. Ao medir a temperatura de um gás durante um experimento, um cientista encontrou o valor de 40°C. Como a unidade de medida de temperatura no sistema internacional é Kelvin, ele precisou realizar a conversão entre as escalas antes de realizar seus cálculos. Qual era a temperatura do gás em Kelvin?
Aplicando a relação entre Kelvin e Celsius, temos:
A temperatura do gás era de 313K.
Um fenômeno comum em nosso cotidiano é a variação de temperatura (∆T), que acontece ao longo do dia, tanto que a previsão do tempo nos fornece, geralmente, a temperatura mínima e a máxima para determinado dia. A variação de temperatura é obtida pela diferença entre a temperatura final e a inicial, de um corpo ou ambiente.
Essa variação pode ser calculada em diferentes escalas e podemos utilizar a seguinte relação para converter as variações de temperatura entre as escalas Celsius, Fahrenheit e Kelvin:
3. Na cidade do Rio de Janeiro, foram registradas as seguintes temperaturas, às 6h da manhã 25°C e às 14h 40°C. Calcule a variação de temperatura nesse dia, em Celsius, Kelvin e Fahrenheit.
Primeiramente, calcularemos a variação em graus Celsius:
Agora, observe a relação entre as variações de temperatura em graus Celsius e em Kelvin:
A conclusão é que a variação da temperatura em Celsius é a mesma quando convertida em Kelvin, logo ∆K = 15K
Por fim, utilizaremos a relação entre a variação de temperatura em Celsius e Fahrenheit:
Assim como a temperatura, em ambientes, por exemplo, pode variar, aprendemos a realizar o cálculo dessa variação e conhecemos uma relação matemática entre as variações de temperatura em diferentes escalas termométricas.
Neste tema, estudamos a definição de temperatura e vimos que é uma medida do grau de agitação das moléculas (ou átomos) que compõem um sistema, ou ainda, a energia cinética dessas moléculas.
Compreendemos o funcionamento de um termômetro, conhecemos diferentes tipos desse aparelho e evidenciamos a relação do termômetro a gás com a escala absoluta e como esse dispositivo se baseia no fato de a pressão absoluta do gás, confinado em seu recipiente, aumenta linearmente quando a temperatura aumenta.
Pudemos ver que existem diversas escalas termómétricas e estabelecemos uma relação matemática capaz de fornecer uma conversão de temperatura entre as escalas mais utilizadas no mundo, as escalas Celsius, Fahrenheit e Kelvin.
Afinal, ressaltamos que a escala Kelvin é definida em termos de uma temperatura chamada zero absoluto, que é a menor temperatura possível, onde cessa o movimento atômico.
Tema 2 - Quantidade de Calor e Transferência de Calor
Neste tema, iniciaremos nosso estudo de calorimetria, a área da física que busca compreender como funciona a troca de energia térmica entre os corpos, ou seja, compreenderemos os fenômenos relacionados às trocas de calor.
Aprenderemos a definição do conceito de calor, veremos a diferença entre calor e temperatura e se existe alguma relação entre ambos.
Veremos que o calor é uma forma de energia e que pode ser transferido de um sistema para outro por três formas distintas:
- 1. condução;
- 2. convecção;
- 3. irradiação.
Analisaremos as grandezas envolvidas nas trocas de calor, por exemplo, calor específico, temperatura e capacidade térmica e introduziremos o conceito de equilíbrio térmico.

Figura 9: Os fatores envolvidos com as trocas de calor. Fonte: Dreamstime.
Poderemos compreender o que acontece com uma substância que recebe ou cede calor sem mudar de estado físico e também os fatores envolvidos com as trocas de calor que resultam em mudança de fase.
Definiremos calor sensível e calor latente e aplicaremos as equações que quantificam esses tipos de calor. Finalmente, faremos uma análise da curva de aquecimento da água a fim de compreender como a temperatura varia e quando ocorrem as mudanças de fase a medida que a substância recebe calor.
Calor
O calor é biologicamente essencial e não haveria vida em nosso planeta se não fosse pelo calor do sol. O calor também está envolvido no funcionamento de motores e circuitos elétricos, por exemplo, e tanto a engenharia quanto várias áreas da ciência precisam trabalhar com o calor num dado momento, o que torna esse tema de suma importância para a pesquisa e desenvolvimento.
Um corpo em combustão, como uma fogueira, não tem calor, e sim, emite calor ao ambiente ao seu redor, então, para que não fiquem dúvidas conceituais ou linguísticas, iniciaremos com a definição de calor e suas unidades de medida.
Ao colocarmos um copo com uma bebida gelada sobre a mesa, é possível observar que a bebida vai aquecendo, lentamente, até chegar à temperatura do ar ambiente. Coisa semelhante ocorre se pusermos um copo com bebida bem quente, ela se resfriará, lentamente, até que esteja à temperatura do ar ambiente.
Esse processo de aquecer ou esfriar acontece de forma mais rápida no início e posteriormente ocorre de forma mais lenta, até que ocorra o equilíbrio térmico entre a bebida e o ambiente, ou seja, a bebida, o copo e o ar ambiente passam a ter a mesma temperatura.
Vamos partir do pressuposto de que o copo com água é o sistema. Essa mudança de temperatura do sistema ocorre devido a troca de energia entre o sistema e o ambiente. Para ser mais específico, essa energia transferida do sistema para o ambiente, quando há diferença de temperatura entre eles, é o chamado calor.

Figura 10: A troca de energia entre o sistema e o ambiente. Fonte: Dreamstime.
O calor, representado pela letra Q, é a energia transferida entre o sistema e o ambiente, por conta da diferença de temperatura entre eles. Quando o sistema recebe calor do ambiente, Q>0 e quando o sistema cede calor para o ambiente, Q<0 .
Para definir a diferença entre sistema e ambiente, vale partir da ideia de que o ambiente é tão grande em comparação ao sistema, que o sistema é praticamente incapaz de alterar, significativamente, sua temperatura.
Como o calor é energia em trânsito, possui, no SI, unidade de medida semelhante à das outras formas de energia, Joule (J). Entretanto, a unidade chamada caloria (cal) é amplamente utilizada e sua conversão nas unidades do SI é dada por:
1 cal = 4,18 J
A palavra calor é usada, geralmente, para expressar que algo está “quente”, como se calor e quente fossem sinônimos.
Curiosidade
A caloria que conhecemos, relacionada aos alimentos, é diferente da caloria térmica. A caloria alimentar, abreviada por Cal (c maiúsculo), é definida da seguinte forma: 1 caloria alimentar = 1 Cal = 1000 cal = 1 kcal = 4186 J
Por exemplo, é muito comum em dias de altas temperaturas reclamarmos dizendo que está “muito calor” e esse tipo de expressão é uma espécie de herança da época em que se pensava que calor fosse uma substância, um tipo de fluido.
Mas o problema com o calor não é apenas linguístico, é também conceitual, pois ainda há uma confusão entre os conceitos de temperatura, calor e energia térmica.
Como essas grandezas estão relacionadas é muito importante que conheçamos suas definições para que não cometamos erros.
Exemplificando, se um bloco desliza em uma superfície e por conta do atrito vem a parar, não é incomum se ouvir que a energia cinética do bloco foi convertida em calor, o que está incorreto, uma vez que não ouve transferência de energia devida à diferença de temperatura. O que ouve foi que a energia mecânica do bloco foi convertida em energia térmica dos átomos e moléculas do corpo.
Resumindo brevemente esses conceitos, temos que a energia térmica é uma energia do sistema e que está relacionada ao movimento aleatório dos seus átomos e moléculas e é uma variável de estado, é usada para descrever o estado de um sistema. Essa energia existe ainda que o sistema esteja isolado termicamente e não troque calor.
O calor, como vimos, é uma forma de energia, que flui de um corpo para outro, ou ainda, que é transferida entre o sistema e sua vizinhança, desde que haja diferença de temperatura entre eles.

Figura 11: O calor como forma de energia. Fonte: Dreamstime.
Se um sistema, nem cede e nem recebe calor da vizinhança, Q = 0 e, embora o calor possa fazer a energia térmica variar, não são a mesma coisa. A temperatura é uma medida do grau de agitação das moléculas de um sistema e é uma variável de estado.
O calor pode ser transferido entre um sistema e sua vizinhança por meio de três mecanismos distintos:
Sendo assim, a transferência de calor por meio de radiação é o que permite que nosso planeta seja aquecido pelo sol, que emite calor por meio da radiação.
Variação de Temperatura e Calor Específico
A partir de agora, veremos o que acontece a um sistema quando adicionamos ou retiramos energia dele, ou seja, quando sua energia térmica varia. De antemão, é possível considerar duas possibilidades: a temperatura do sistema irá se alterar;
O sistema sofrerá uma mudança de fase, por exemplo, fusão ou solidificação. Tendo em mente essa primeira possibilidade, vamos supor um sistema que consiste em uma amostra de uma certa substância.
Se um sistema é composto por uma substância, existe uma certa quantidade de energia necessária para fazer que a temperatura de certa massa da substância se eleve de um determinado valor.
Em outras palavras, se temos uma massa de água de 1Kg, e desejamos elevar a temperatura dessa massa de 1°C, é necessário fornecer 4186J de energia para isso.
Mas se, ao invés de água, tivermos 1kg de cobre, para elevar sua temperatura de 1°C, será necessário apenas 387J de energia. Para sermos mais exatos, chamaremos essa energia de calor.
A grandeza que especifica quanto calor é necessário para elevar a temperatura de uma amostra de 1°C é chamada Capacidade térmica, representada por c maiúsculo. A capacidade térmica é dada por
Sua unidade de medida é J/K (Joule por Kelvin).
Um detalhe ainda não foi esclarecido: por que essa quantidade de calor necessária para elevar de 1°C, 1 Kg de uma amostra varia de substância para substância?
A medida da sensibilidade térmica que uma substância possui, ou seja, a facilidade para se elevar ou diminuir sua temperatura, é dada pelo calor específico do material, representado por c minúsculo. O calor específico é dado por
No SI, a unidade do calor específico é J/(kg.K), mas em aplicações práticas, o calor específico, geralmente, está em cal/(g.K)°C ou ainda cal/g.°C.
Importante
Podemos usar as unidades J/(kg.K) e J/(kg.°C) de forma intercambiável para o calor específico, já́ que é definido em termos da variação de temperatura.
| Calor Específico de algumas substâncias | ||
|
Calor específico c |
||
|
Material |
KJ/Kg.K |
Cal/g.k |
|
chumbo |
0,129 |
0,0308 |
|
cobre |
0,386 |
0,0922 |
|
aço |
0,448 |
0,107 |
|
alumínio |
0,900 |
0,215 |
|
vidro |
0,840 |
0,20 |
|
gelo |
2,06 |
0,500 |
|
água |
4,186 |
1,00 |
|
vapor |
2,01 |
0,48 |
Tabela 1: Calor específico de substâncias selecionadas. Fonte: Adaptada de Bauer; Westfall; Dias (2012, p. 200).
A quantidade de calor transferida entre os corpos, que provoca mudança de temperatura, é conhecida como Quantidade de Calor Sensível e pode ser calculada da seguinte forma
Q = m.c. ∆T
Importante
Sabemos que, na prática, ∆T é expressa em °C, mas vale lembrar que as escalas de temperatura Celsius e Kelvin tem intervalos iguais, de modo que ∆T expressa em K tem valor numérico exatamente igual que ∆T em °C. Sendo assim, não é necessário converter as temperaturas de °C para K quando precisamos apenas de uma variação de temperatura ∆T
Vejamos um exemplo de aplicação da equação da quantidade de calor sensível.
1. Calcule a quantidade de calor necessária para elevar a temperatura de uma massa de 1Kg de água, inicialmente a 10°C, para 20°.
Dado: calor específico da água 4186J/Kg.°C.
Vamos aplicar a equação para cálculo de quantidade de calor sensível, lembrando que a variação de temperatura ∆T = Tfinal – Tinicial
Q = m. c. ∆T
Q = 1. 4186. (20 – 10)
Q = 41860 J
Quando se deseja descobrir o calor específico de uma amostra utiliza-se uma técnica chamada de calorimetria, que consiste em colocar a amostra em um recipiente contendo água, em quantidade e temperatura conhecidas, e após o equilíbrio térmico mede-se a temperatura da água novamente.
Essa transferência de calor ocorre em um recipiente isolado termicamente chamado calorímetro.
Quando dois corpos com temperaturas diferentes são postos dentro de um calorímetro, o calor sempre irá fluir do corpo de maior temperatura para o corpo de menor temperatura (Figura 12) até que os dois corpos atinjam a mesma temperatura.
Como nenhum calor irá fluir para dentro ou para fora do calorímetro, o calor cedido pela substância mais quente será́ igual ao calor recebido pela substância mais fria (lei da conservação de energia).
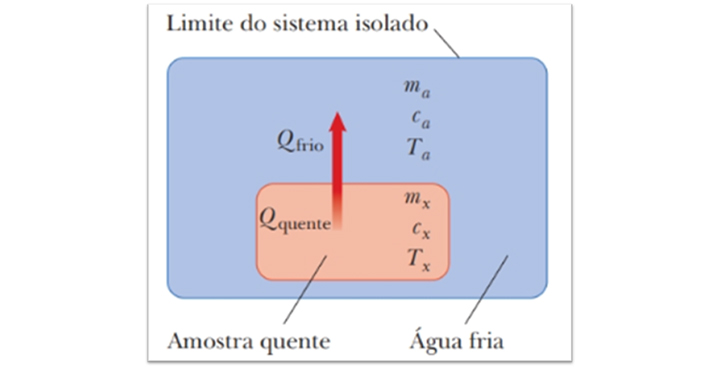
Figura 12: Amostra de substância desconhecida posta em um calorímetro contendo água, a
temperatura da amostra é superior que a da água. Fonte: Jewett Jr.; Serwat (2013, p.
137).
A lei da conservação da energia nos permite escrever que:
Qfrio = Qquente
Admitiremos que a massa, o calor específico e a temperatura inicial da substância desconhecida sejam, respectivamente, mx ,cx e Tx , como mostrado na Figura 12, e a massa, o calor específico e a temperatura inicial da água sejam, respectivamente, ma, ca e Ta. Se Tf é a temperatura final, ou temperatura do equilíbrio, substituindo essas expressões na equação acima, temos
Qfrio = Qquente
maca(Tf – Ta) = – mxcx(Tf – Tx)
Resolvendo essa equação, é possível encontrar o calor específico desconhecido cx
Calor Latente e Mudança de Fase
Destacamos agora que uma substância pode sofrer uma variação em sua temperatura após trocar calor com sua vizinhança.
Mas, em algumas situações, a transferência de calor não irá provocar uma variação na temperatura, nesse caso, ocorrerá mudança nas características físicas da substância, o que chamamos de mudança de fase.
Importante
Durante a mudança de fase, a temperatura de um corpo permanece constante.
Existem três estados conhecidos da matéria (sólido, líquido e gasoso), e as mudanças de fase de nosso interesse são a fusão, a solidificação, a ebulição (ou vaporização) e a condensação, como mostra a figura abaixo.
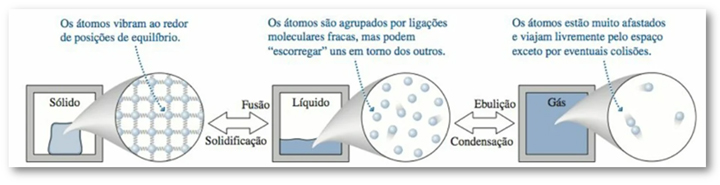
Figura 13: Os três estados da matéria. Fonte: Knight (2009, p. 62).
A quantidade de calor necessária para provocar uma mudança de fase é chamada de Quantidade de Calor Latente e é dada por meio da equação.
Q = m . L
Onde m é a massa da substância e L é o calor latente. O valor de L para uma substância irá depender da natureza da mudança de fase (fusão, solidificação, ebulição ou condensação) e das propriedades da substância.
O termo L, calor latente, é utilizado da seguinte forma:
- • se a mudança de fase ocorrida for a fusão utilizaremos o Lf, calor latente de fusão;
- • se a mudança de fase for a vaporização, utilizaremos o Lv, calor latente de vaporização.
O calor necessário para essas mudanças de fase é dado então por:
Onde o símbolo ± indica que o sistema recebe calor durante uma fusão ou vaporização e que o sistema perde calor durante uma solidificação ou condensação. Então, devemos incluir o sinal negativo explicitamente quando for necessário.
Curiosidade
A temperatura em que um sólido derrete e vira líquido é chamada de ponto de fusão, Tfusão. A temperatura em que um líquido evapora e vira um gás é chamada de ponto de ebulição, Tebulição.
Observe o exemplo para compreender o papel do calor latente nas mudanças de fase.
Exemplo
Qual a quantidade de calor necessária para transformar 0,2 Kg de gelo em água a 0°C? Dado: Calor latente de fusão da água Lf = 3,33. 105 J/Kg.
Aplicando a equação da quantidade de calor latente e substituindo os dados do enunciado, temos:
Temos ainda um interessante recurso para analisar as variações sofridas por uma substância quando sua energia térmica se altera, a curva de aquecimento. A curva de aquecimento de uma sustância (Figura 14) é de suma importância, pois evidencia as mudanças sofridas pelo material, sejam mudanças de fase ou de temperatura, à medida que a amostra recebe calor.
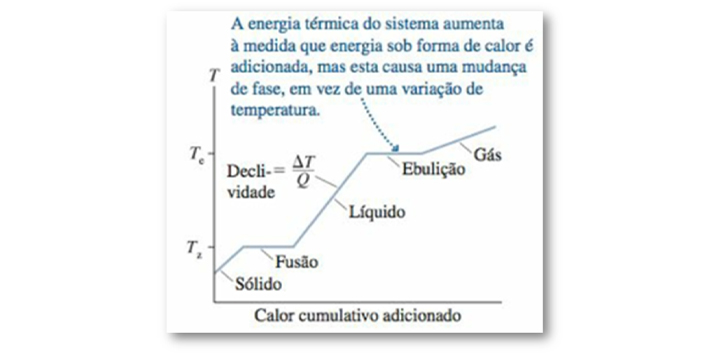
Figura 14: Curva de aquecimento de uma substância. Fonte: Knight (2009, p. 101).
Observe que o gráfico apresenta inclinações diferentes, essas diferentes declividades indicam para nós que as fases sólida, líquida e gasosa de uma substância apresentam calores específicos diferentes.
Em contrapartida, existem momentos em que o gráfico apresenta segmentos de reta horizontais, que indicam que o calor é transferido para o sistema, mas sem que sua temperatura sofra variação. Esses trechos correspondem as mudanças de fase, pois ocorrem a temperatura constante.
A energia térmica do sistema continua aumentando durante as mudanças de fase, mas o calor recebido serve apenas para quebrar as ligações moleculares e não aumentar a agitação dessas moléculas.
Vejamos um exemplo para compreender como se utilizar a curva de aquecimento da água.
Exemplo (adaptado de Jewett Jr.; Serwat, 2013, p.140):
Observe a curva de aquecimento da água fornecida abaixo. Calcule a quantidade de calor necessária para elevar a temperatura de 1.10-3 Kg de água de 0°C a 100 °C e transformá-la em vapor.
Veja se corresponde à quantidade de calor fornecida pela curva.
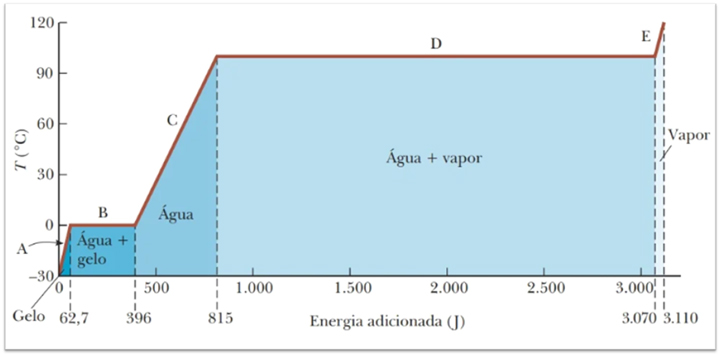
Figura 15: Curva de aquecimento água. Fonte: Jewett Jr.; Serwat (2013, p. 140).
Dados: Calor específico da água ~ 4,19.103 J/ Kg.°C; calor latente de vaporização Lv = 2,255.106 J/kg.
Primeiramente, vamos calcular a quantidade de calor sensível para elevar a temperatura da água de 0 °C a 100°C.
Q = m.c.∆T
Q = 1.10-3. 4,19.103. (100 – 0)
Q = 419 J
Agora, calcularemos a quantidade de calor latente para realizar a vaporização da água que já elevamos aos 100°C
Q = m.Lv
Q = 1.10-3. 2,255 ́106
Q = 2,255.103J
Q = 2255 J
Como durante a mudança de fase a temperatura não se altera, o vapor terá 100°C. A quantidade de calor total será dada pela soma da quantidade de calor sensível com a latente
Qtotal = 419 + 2255
Qtotal = 2674 J
Observando o gráfico, vemos que quando a água estava a 0°C o calor era 396J, e quando se tornou vapor a 100°C, o calor era 3070J, então Q = 3070 – 396 = 2674J, o mesmo valor encontrado em nossos cálculos.
Assim, podemos concluir que como o calor flui entre sistema e vizinhança, desde que haja diferença de temperatura eles, após o equilíbrio térmico o calor cessa, ou seja, não haverá mais essa transferência de energia.
Neste tema, estudamos o conceito de calor, que é uma energia que flui entre os corpos quando há uma diferença de temperatura entre eles, até que ocorra o equilíbrio térmico. Estabelecemos as diferenças entre calor, temperatura e energia térmica, que embora estejam relacionadas, não são a mesma coisa.
Vimos que se uma substância recebe calor sua energia térmica aumenta, o que não irá provocar, necessariamente, um aumento de temperatura. Uma variação de energia térmica, ou alterará o grau de agitação das moléculas (temperatura) ou alterará as ligações moleculares e a substância mudará de fase.
Aprendemos que o calor sensível é a quantidade de calor necessária para que haja variação de temperatura do material e que a quantidade de calor necessária para elevar a temperatura da susbtância em 1K é dada pela capacidade térmica. A propriedade da matéria que determina sua sensibilidade térmica é o calor específico c, e cada substância tem um valor para ele.
Finalmente, vimos que o calor latente é a quantidade de calor necessária para que haja mudança de fase da substância e analisamos uma curva de aquecimento, que é uma representação gráfica das sucessívas mudanças de temperatura e de fase que uma amostra sofre ao receber calor.
Tema 3 - Dilatação Térmica dos Sólidos, Líquidos e Gases
Neste tema, compreenderemos como uma variação de temperatura pode provocar mudanças nas dimensões de um corpo.
Em nossos estudos, já definimos que a temperatura é a medida do grau de agitação dos átomos, ou moléculas que compõem um corpo. Se essa agitação molecular aumentar, ou seja, se a temperatura do corpo aumentar, essas moléculas de chocarão aleatóriamente e se afastarão.

Figura 16: Molécula de água hidrogênio átomos de oxigênio moléculas. Fonte: Dreamstime.
O contrário também acontece: se essas moléculas começarem a se mover mais lentamente, por conta de uma diminuíção de temperatura, os choques diminuirão. Esses fenômenos resultam em uma alteração nas dimensões de um material e esse efeito nem sempre é desejável.
Então, analisaremos esses efeitos que são resultado da mudança de temperatura sofrida por um corpo e aprenderemos a calcular a variação de tamanho resultante desse processo.
Essa variação de tamanho pode acontecer no comprimento, área ou volume do corpo e é de suma importância para diversas áreas da engenharia, já que pode ajudar a prevenir deformações indesejadas, contribuindo para uma melhor escolha de material para um projeto.
Dilatação Térmica dos Sólidos
Quase todos nós estamos familiarizados, em algum nível, com o fenômeno da dilatação térmica. A dilatação térmica pode ser colocada em prática quando precisamos abrir uma tampa de metálica de um pote de vidro e a mergulhamos em água quente para afrouxar.
Mas o resultado da dilatação nem sempre é desejável, já que pode provocar danos nas estruturas das construções, por exemplo, as pontes das estradas costumam ter fendas de dilatação (Figura 17) para permitir a expansão do material de acordo com a variação de temperatura.

Figura 17: Fenda de dilatação. Fonte: Dreamstime.
As tubulações das refinarias também precisam desse tipo de fenda de expansão para evitar que ocorra a flambagem (deformação lateral) do encanamento com o aumento da temperatura.
Importante
Para se ter ideia da importância da escolha do material, quanto à sua expansão térmica, até mesmo o material utilizado para restaurações dentárias precisa ter suas propriedades de dilatação semelhantes às do esmalte dos dentes.
Também é possível tirar vantagem do processo de dilatação, o que ocorre na fabricação de aviões, onde algumas peças de fixação são resfriadas com gelo seco, para contrair antes de sua colocação, e quando colocadas dilatam produzindo um ajuste firme.
A Figura 18 mostra o efeito da dilatação em lâminas bimetálicas em forma de hélice, que são utilizadas em termômetros comuns e podem se enrolar e desenrolar com as mudanças de temperatura.
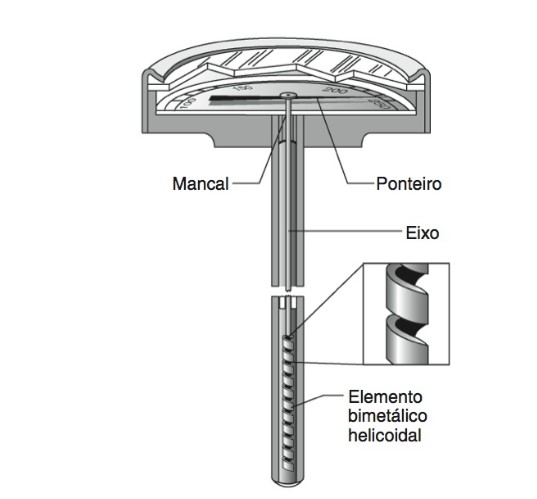
Figura 18: Termômetro de lâmina bimetálica. Fonte: Halliday; Resnick; Krane (2017, p.
212).
Os termostatos de equipamentos domésticos, por exemplo, se beneficiam da expansão térmica a partir da curvatura que a lâmina bimetálica sofre com o aumento de temperatura (Figura 19), o que ocorre por conta das diferentes propriedades de seus componentes. Quando a temperatura se eleva, a lâmina encurva e esse movimento é utilizado para abrir e fechar um circuito elétrico.
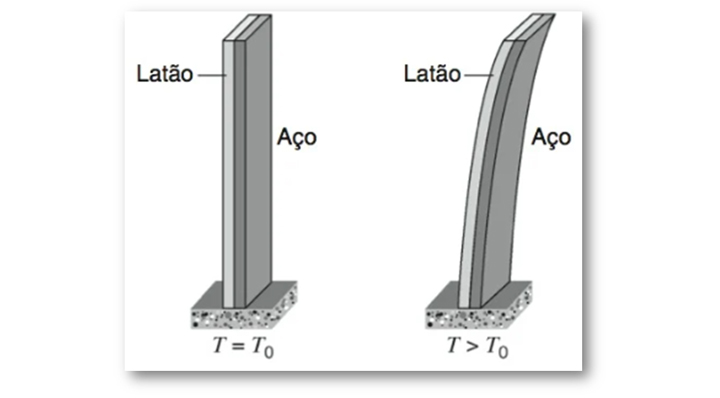
Figura 19: Dilatação de uma lâmina bimetálica. Fonte: Halliday; Resnick; Krane (2017, p.
212).
A dilatação térmica é uma consequência de um afastamento que ocorre entre os átomos de um corpo.
Para facilitar a compreensão desse fato, podemos imaginar que os átomos são conectados por molas rígidas (Figura 20) e que quando estão sob temperaturas normais, oscilam em torno de suas posições de equilíbrio com uma amplitude de cerca de 1011m, frequência de 1013 Hz e com afastamento médio entre os átomos de cerca de 1010m.
Entretanto, à medida que a temperatura do corpo sólido aumenta, a amplitude da oscilação dos átomos também aumenta e por consequência, aumenta o afastamento dos átomos, logo o corpo sofre expansão, ou dilatação.
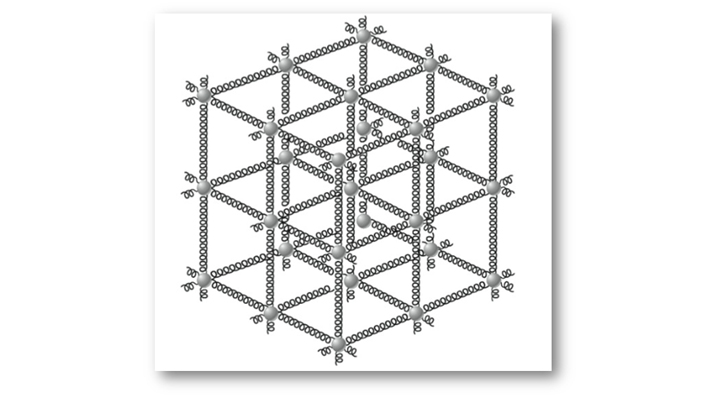
Figura 20: Átomos de um sólido comportando-se como se fossem presos a molas. Fonte:
Halliday; Resnick; Krane (2017, p. 213).
Dilatação Térmica em uma, duas e três Dimensões
Se a variação da dimensão de um corpo ocorrer em apenas uma dimensão, em seu comprimento, por exemplo, a expansão será chamada de Dilatação Linear (∆L). O cálculo da dilatação linear é feito pela equação:
∆L = Lo.α.∆T
Onde,
∆L: é a variação de comprimento (Lfinal – Linicial);
Lo: é o comprimento inicial do objeto;
α: é o coeficiente de dilatação linear;
∆T: é a variação da temperatura (Tfinal - Tinicial).
Importante
A equação da dilatação pode ser usada para a dilatação térmica, quando a temperatura do material aumenta, e para a contração térmica, quando sua temperatura diminui. Havendo contração do material ∆L terá valor negativo.
O coeficiente de dilatação linear depende da substância que compõem o corpo e é a variação fracionária do comprimento pelo grau de variação da temperatura. Reescrevendo a equação acima, o coeficiente de dilatação linear é dado por:
Observe, na tabela abaixo, o coeficiente de dilatação linear de alguns materiais comuns:
| Material | α = (10-6 °C-1) |
Alumínio |
22 |
Latão |
19 |
Concreto |
15 |
Cobre |
17 |
Diamante |
1 |
Ouro |
14 |
Chumbo |
29 |
Vidro Laminado |
9 |
Borracha |
77 |
Aço |
13 |
Tungstênio |
4,5 |
Tabela 2: Coeficientes de dilatação linear de materiais selecionados. Fonte: Bauer; Westfall; Dias (2012, p. 174).
Exemplo
Uma barra de alumínio de comprimento inicial Lo = 1 m estava inicialmente a uma temperatura de 25°C. Qual será o comprimento final da barra quando tiver sua temperatura elevada para 100°C? Dados: α = 22. 10-6 °C-1.
O comprimento final da barra será dado pela soma entre o comprimento inicial e o valor dilatado:
Com as informações vistas até aqui, já podemos aprofundar a questão da dilatação das lâminas bimetálicas. A lâmina bimetálica, como mostra a Figura 21, é constituída por dois materiais, aço e latão, que possuem diferentes coeficientes de dilatação linear. Conforme lista a Tabela 2, αlatão > αaço, logo, a dilatação do latão será maior que a do aço e a lâmina se encurvará em direção ao lado do aço.
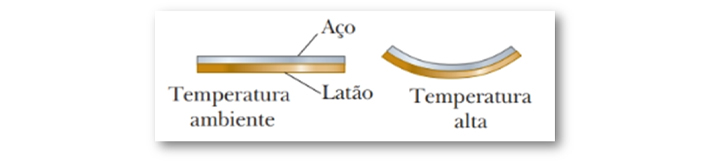
Figura 21: Lâmina bimetálica composta por aço e latão. Fonte: Jewett Jr.; Serwat (2013,
p. 119).
A temperatura também exerce influência sobre a área de um objeto (Figura 22), então se a variação do tamanho de um corpo ocorrer em duas dimensões linearmente em função da variação de temperatura, a expansão será chamada de Dilatação Superficial (∆L).
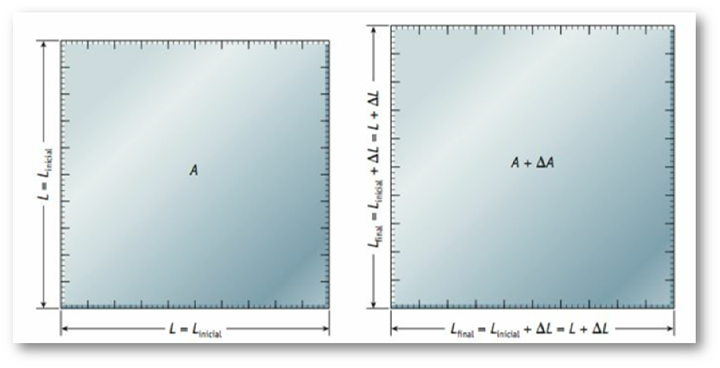
Figura 22: Dilatação superficial de uma placa de lado L. Fonte: Bauer; Westfall; Dias
(2012, p. 177).
O cálculo da dilatação superficial, ou dilatação da área, é feito por meio da equação:
Onde,
∆A: é a variação de área (Afinal – Ainicial);
Ao: é área inicial do objeto;
β: é o coeficiente de dilatação superficial;
∆T: é a variação da temperatura (Tfinal - Tinicial).
O valor do coeficiente de dilatação superficial é o dobro do valor numérico do coeficiente de dilatação linear β = 2α.
Se a temperatura de um corpo aumenta, cada dimensão linear do corpo aumenta de tamanho, isso inclui qualquer buraco que haja na peça. Em resumo, a dilatação de placas com orifício acontecerá da seguinte maneira, a área vazada da peça dilatará como se fosse preenchida de material.
Tanto a placa quanto o orifício aumentarão proporcionalmente à variação de temperatura. Observe, na Figura 23, a dilatação térmica de uma arruela metálica homogênea quando aquecida
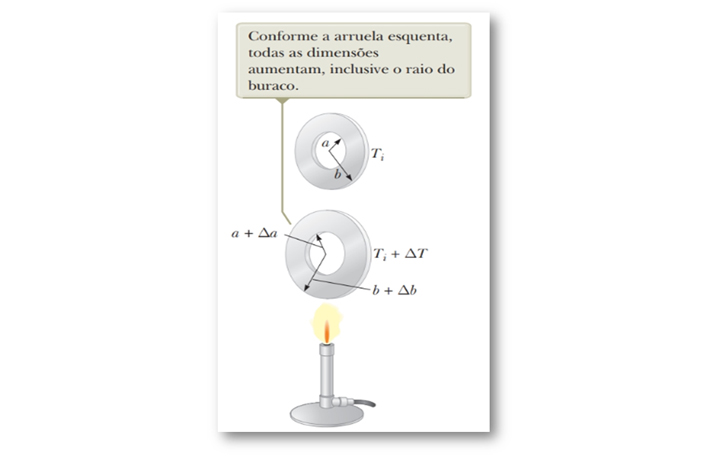
Figura 23: Dilatação superficial de uma arruela metálica com orifício. Fonte: Jewett
Jr.; Serwat (2013, p. 117).
Exemplo:
Uma chapa de cobre, com β = 34.10-6°C-1, sofre uma elevação de 70°C em sua temperatura. Sabendo que a área inicial da chapa era 100cm2, calcule a dilatação superficial da chapa.
Aplicaremos a equação da dilatação superficial e substituiremos os dados fornecidos no enunciado do problema:
A chapa de cobre sofreu uma dilatação de 0,238 cm2 em sua área. Para obtermos o valor da área final da chapa, após a dilatação, basta somar o valor de ∆A à sua área inicial Ao.
Curiosidade
O resultado de uma variação de temperatura sobre a área de um objeto é similar a usar um fotocopiadora para ampliar ou reduzir uma foto, pois cada dimensão do objeto se alterará linearmente de acordo com a variação de temperatura.
Agora, iremos considerar que se as dimensões lineares de um corpo mudam com a temperatura, o seu volume também muda.
Então, se um corpo sofre mudança em suas três dimensões, comprimento, largura e altura, a expansão térmica será chamada de Dilatação Volumétrica (∆V).
Para calcular a dilatação volumétrica de um corpo, utilizaremos uma equação análoga às equações da dilatação linear e superficial, a equação da dilatação volumétrica:
Onde
∆V: é a variação de volume (Vfinal – Vinicial);
Vo: é o volume inicial do objeto;
γ: é o coeficiente de dilatação volumétrica;
∆T: é a variação da temperatura (Tfinal - Tinicial).
A equação da dilatação volumétrica aplica-se à expansão térmica da maioria dos sólidos e líquidos. No entanto, ela não a descreve a expansão térmica da água.
Os coeficientes de dilatação volumétrica relacionam-se entre si da seguinte forma:
De forma simplificada, podemos relacionar os três:
| Material | Coeficientes γ (10-6°C-1) °C-1) |
|
Mercúrio |
181 |
|
Gasolina |
950 |
|
Querosene |
990 |
|
Álcool Etílico |
1120 |
|
Água (1°C) |
-47,8 |
|
Água (4°C) |
0 |
|
Água (7°C) |
45,3 |
|
Água (10°C) |
87,5 |
|
Água (15°C) |
151 |
|
Água (20°C) |
207 |
Tabela 3: Coeficientes de dilatação volumétrica de alguns líquidos comuns. Fonte: Fonte: Adaptada de Bauer; Westfall; Dias (2012, p. 179).
Vejamos um exemplo de aplicação da equação da dilatação volumétrica
1. Um motorista leva seu carro para abastecer, com gasolina γ = 950.10-6 °C-1, em um dia de verão quando os termômetros marcavam 40°C. O volume do tanque do carro é de 60L e foi completamente cheio de gasolina que estava a 10°C armazenada em um reservatório subterrâneo.
Sabendo que o motorista estacionou em um restaurante ao lado do posto de gasolina para almoçar e que quando saiu observou que o combustível do havia transbordado um pouco, calcule a quantidade de gasolina que transbordou, ou seja, dilatou.
Sabemos que, no decorrer do tempo, a gasolina trocou calor com o ambiente até alcançar o equilíbrio térmico e atingir 40°C; com isso, temos que ∆T = 40 – 10 = 30°C. Então, aplicando a equação da dilatação volumétrica, temos:
Sendo assim, o volume da gasolina aumentou em 1,71 litro conforme a temperatura da gasolina subiu de 10°C para 40°C.
Como o tanque de combustível já estava cheio quando a temperatura da gasolina era de 10°C, o excesso de volume transbordou do tanque.
Os líquidos, que, em geral, possuem coeficiente de dilatação cerca de dez vezes maior que o dos sólidos, costumam dilatar com o aumento de temperatura, mas a água fria é uma exceção.
Isso pode ser constatado a partir da curva de densidade versus temperatura, como mostra a Figura 24.
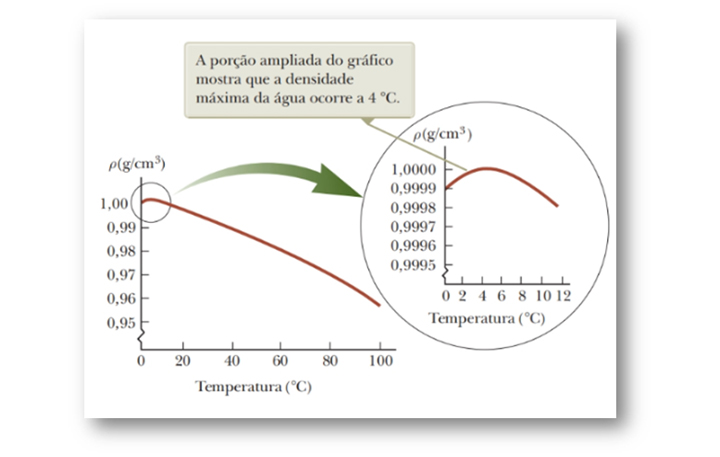
Figura 24: Curva de densidade versus temperatura da água. Fonte: Jewett Jr.;
Serwat
(2013, p. 120).
Observando a curva, podemos notar que quando a temperatura aumenta de 0°C para 4°C, a água se contrai e a sua densidade aumenta. Mas, quando atinge temperatura acima de 4°C, a água se expande com o aumento de temperatura, logo, sua densidade diminui. Podemos concluir que a densidade da água atinge seu valor máximo, 1,000 g/cm3, quando está a 4°C.
Esse comportamento incomum de dilatação térmica da água pode explicar o fato de uma lagoa começar a congelar pela superfície e não pelo fundo.
Pensemos no seguinte exemplo: se a temperatura do ar cair de 7 °C para 6 °C, a água da superfície também irá esfriar, logo, seu volume irá diminuir.
Como a água da superfície ficará mais densa que a água abaixo dela, que não sofreu resfriamento e diminuição de volume, irá descer mais para o fundo, e a água mais quente se moverá para a superfície.
Entretanto, quando a temperatura do ar estiver entre 4°C e 0°C, a água da superfície irá dilatar conforme seu resfriamento e ficará menos densa que a abaixo dela e o processo de mistura irá cessar e a água da superfície congelará.
Como o gelo é menos denso que a água, à medida que a água congela, permanece na superfície. O gelo continuará a se acumular nela, mas a água na região mais funda permanecerá a 4°C, esse comportamento anômalo da água favorece a sobrevivência de peixes e outros seres marinhos.
Quanto aos gases, é preciso compreender que eles podem se expandir de diversas maneiras, pois a pressão e o volume podem até variar simultaneamente, a princípio tenha em mente que: se mantivermos a pressão constante o volume do gás irá variar; se o volume for mantido constante o gás exercerá diferentes pressões. Lembrando que o gás é um fluido e que seu volume equivale ao volume do recipiente onde está contido.
A expansão do gás pode ser realizada confinando-o em um cilindro fechado com um êmbolo que pode se mover livremente sem atrito e onde a pressão atuante deve ser constante.
A variação do volume desse gás, à pressão constante, pode ser considerada proporcional à variação de temperatura e volume inicial. Então, para um gás inicialmente a 0°C, volume inicial V0 e temperatura final T(°C) a variação do volume ∆V, pode ser dada por
Sendo assim, o coeficiente de dilatação volumétrica γ de um gás ideal, a pressão constante, determinado experimentalmente, é de cerca de 3,66.10-3°C-1.
Neste tema, estudamos a dilatação térmica, uma variação nas dimensões de um corpo que ocorre devido a uma variação de temperatura sorida por ele. Esse fenêmeno pode acontecer em sólidos líquidos e gases.
Em resumo, quando a temperatura de um corpo aumenta suas dimensões aumentam e quando a temperatura de um corpo dimunui suas dimensões também diminuem (contração térmica).
Vimos que com o aumento da temperatura as moléculas do corpo começam a vibrar mais rapidamente, o que provoca mais colisões entre elas, consequentemente, aumenta o afastamento entre essas moléculas e o corpo aumenta de tamanho.
De forma contrária, quando a temperatura diminui, o movimento das moléculas que compõem o corpo fica mais lento, ocorrem menos colisões e o afastamento entre as moléculas é menor, logo, o tamanho do corpo diminui.
A dilatação térmica pode ocorrer em uma, duas ou três dimensões. Chamamos de dilatação linear a dilatação que ocorre em apenas uma dimensão, dilatação superficial quando há aumento em duas dimensões e dilatação volumétrica se o aumento acontece para três dimensões do corpo.
Além da Sala de Aula
Na leitura indicada, o autor aborda os diferentes mecanismos de transferência de energia em processos térmicos. De forma bastante detalhada, explica a condução de calor e como a taxa de condução térmica depende das propriedades da substância sendo aquecida. O autor ainda faz uma excelente contextualização mostrando como esse conhecimento se aplica no isolamento térmico doméstico.
Essa leitura detalhará ainda o processo de convecção, mostrando exemplos de processos de convecção natural, que acontecem de forma espontânea na natureza.
Por fim, o autor abordará o processo de transmissão de calor por irradiação, mostrando como esse conhecimento se aplica no frasco de Dewar, um recipiente isolado termicamente, semelhante às garrafas térmicas de uso doméstico.
Todos esses pontos são tratados por Jewett Jr. e Serwat (2013), por isso, faça a leitura da página 149 a 155 do livro Física para cientistas e engenheiros, disponível na Minha Biblioteca.
Lembre-se de que, para iniciar a leitura do livro sinalizado, é necessário fazer login na Minha Biblioteca.
Título do livro/artigo: Física para cientistas e engenheiros
Páginas indicadas: 149 a 155
Referência (ABNT): JEWETT JR., J. W.; SERWAT, R. A.
Física para cientistas e engenheiros. Oscilações; ondas e
termodinâmica. 2. ed. São Paulo: Cengage Learning Brasil, 2013. v. 2.
Na leitura indicada, os autores abordam a expansão térmica de sólidos e líquidos, ou seja, a variação que um corpo pode sofrer em uma, duas, ou três dimensões, quando sofre uma variação de temperatura.
Os autores abordam de forma bastante clara e objetiva as aplicações da expansão térmica linear, mostrando como esse fenômeno ocorre em uma lâmina bimetálica, comumente utilizada em termostatos.
Eles demonstram, a partir de um exemplo real, como a dilatação dos sólidos impactam as construções civis e apresenta diversos exemplos da dilatação superficial e volumétrica, inclusive, explica como a expansão térmica pode comprovar o aquecimento da superfície terrestre, evidenciando que atividades humanas têm exercido influência na variação de temperatura do planeta Terra.
Todos esses pontos são tratados por Bauer, Westfall e Dias (2012), por isso, faça a leitura da página 177 a 182 do livro Física para universitários, disponível na Minha Biblioteca.
Lembre-se de que, para iniciar a leitura do livro sinalizado, é necessário fazer login na Minha Biblioteca.
Título do livro/artigo: Física para universitários
Páginas indicadas: 177 a 182
Referência (ABNT): BAUER, W.; WESTFALL, G. D.; DIAS, H.
Física
para universitários. Porto Alegre: AMGH, 2012.
A Temperatura como Fator de Segurança em Reatores Químicos
Neste estudo de caso, analisaremos como a temperatura pode ser um fator determinante para o bom funcionamento de um reator químico que opera em um processo de produção de insumos farmacêuticos. Veremos como o conhecimento de diferentes escalas termométricas é fundamental na identificação de riscos na operação de um reator químico evitando acidentes e perdas de produtos.
Considere a seguinte situação: nas indústrias químicas, é comum que se faça uso de equipamentos de outros países, como os Estados Unidos, esses equipamentos utilizam a escala Fahrenheit para medição de temperatura e essa escala é mantida em suas aferições.
Um reator químico, recipiente projetado para ser utilizado para conter reações químicas, é largamente utilizado na produção de medicamentos de uma determinada empresa farmacêutica.
A temperatura nesse reator é medida em fahrenheit, e sabemos que a temperatura é um parâmetro crítico e precisa ser controlada e regulada a fim de garantir não apenas a segurança do processo, mas também para diminuir perdas e baixa produtividade devido a paradas do equipamento.
As reações que ocorrem no reator químico devem ser devidamente controladas, uma vez que esse dispositivo pode representar um risco tanto para os trabalhadores envolvidos no processo quanto para a comunidade vizinha.
Em um dia de produção comum nessa indústria, um determinado intermediário farmacêutico era processado em bateladas, gerando 450 kg de produto em um reator de 2,0 m3 e as temperaturas de operação padrão, fornecidas na escala Celsius devem ser seguidas com a maior exatidão possível.
Referência: VAZ, L. Análise de riscos na operação de um reator químico. 2019. Monografia (Especialização em Engenharia de Segurança do Trabalho) – Universidade de São Paulo, São Paulo, 2019. Disponível em: https://bdta.abcd.usp.br. Acesso em: 9 out. 2024.
Questionamentos para reflexão:
- Há necessidade de converter as temperaturas de operação, que estão em Celsius, para Fahrenheit, a temperatura utilizada pelo reator?
- Qual é a equação que o engenheiro responsável poderia utilizar para fazer as devidas conversões entre as escalas Celsius e Fahrenheit?
- Sabendo que os reagentes devem ser misturados a uma temperatura de 80°C, qual a temperatura, em farenheit deve ser observada no termômetro do reator?
- Após a mistura dos reagentes o aquecimento foi interrompido e a reação prosseguiu por cerca de quinze horas, alcançando uma temperatura máxima de 150 °C, ou seja, era uma reação exotérmica. Sabendo que a temperatura limite para que o reator funcione com segurança é 160°C, o engenheiro responsável fez a verificação do termômetro do equipamento que marcava 300°F. A operação do reator estava oferenco riscos?
Assista às videoaulas a seguir, que têm como objetivo reforçar os conteúdos abordados nesta unidade de maneira didática para embasar os conceitos e teorias trabalhados. Esperamos que contribuam significativamente para seu aprendizado e que a busca pelo conhecimento não se encerre neste percurso de aprendizagem.
Neste infográfico, faremos um resumo das diferentes dilatações térmicas conhecidas. Esse fenômeno pode ocorrer em materiais sólidos, líquidos e gases e é de grande importância para diversas áreas de conhecimento, em especial para a construção civil, em que é necessário escolher os materiais considerando a facilidade que têm para dilatar, já que a dilatação pode provocar rachaduras e outros defeitos estruturais.

Nesta unidade, definimos o conceito de temperatura como uma medida da energia cinética das moléculas que compõem o corpo, ou seja, seu grau de agitação. Verificamos que há diversos tipos de termômetros, formados por diferentes substâncias. Conhecemos as diferentes escalas termométricas, Celsius, Fahrenheit e Kelvin e aplicamos uma relação matemática para converter os valores de uma medida de temperatura de uma escala para a outra.
Definimos o conceito de calor como uma forma de energia que flui entre os corpos quando há uma diferença de temperatura entre eles. Esse trânsito de energia pode ocorrer por três mecanismos diferentes. Quando um corpo recebe ou cede calor, ou sua temperatura se altera, ou o corpo muda de fase. Se a quantidade de calor calculada for positiva, significa que o corpo recebeu calor, mas se for negativa, então o corpo cedeu calor.
Pudemos observar que uma variação de temperatura pode alterar as dimensões de um corpo e aprendemos as equações que nos permitem calcular o quanto um corpo dilatou. Essas equações dependerão do coeficiente de dilatação do material que compõem o corpo, das dimensões iniciais e da variação de temperatura.
Para sua autorreflexão:
- Conseguiu aplicar a equação para converter valores de temperatura entre as escalas?
- Identificou como se deve calcular a quantidade de calor recebida ou cedida pelo corpo?
- Entendeu o processo de cálculo das equações para a dilatação linear, superficial e volumétrica?
BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: AMGH, 2012.
HALLIDAY, D.; RESNICK, R.; KRANE, K. S. Física. 5. ed. Rio de Janeiro: LTC, 2017. v. 2.
IFSC. Processos térmicos em gases. Laboratório de Física II, 2020. Disponível em: https://edisciplinas.usp.br/pluginfile.php/5845999/mod_resource/content/1/PRATICA%20VI.pdf. Acesso em: 9 out. 2024.
JEWETT JR., J. W.; SERWAT, R. A. Física para cientistas e engenheiros. Oscilações; ondas e termodinâmica. 2. ed. São Paulo: Cengage Learning Brasil, 2013. v. 2.
KNIGHT, R. D. Física uma abordagem estratégica: termodinâmica óptica. 2. ed. Porto Alegre: Bookman, 2009. v. 2.
OLIVEIRA, F. S. de. Termologia. IFUSP, 2015. Disponível em: https://edisciplinas.usp.br/pluginfile.php/324050/mod_resource/content/1/Material%20Did%C3%A1tico%20-%20Francisco.pdf. Acesso em: 9 out. 2024.
VAZ, L. Análise de riscos na operação de um reator químico. 2019. Monografia (Especialização em Engenharia de Segurança do Trabalho) – Universidade de São Paulo, São Paulo, 2019. Disponível em: https://bdta.abcd.usp.br/directbitstream/3a53804a-984a-4636-8164-ed174dc4fad8/LEONARDO%20TAVARES%20ESTEVES%20VAZ.PDF. Acesso em: 9 out. 2024.







