Nesta unidade, estudaremos um dos movimentos mais importantes da física, o movimento harmônico simples (MHS). O MHS além de estar aplicado a diversos fenômenos que podemos visualizar também é um excelente exemplo de aplicação das leis da mecânica, pois coloca de forma mais clara como identificar a posição de uma partícula, uma vez que conhecemos as forças que atuam sobre ela. Compreenderemos a natureza do movimento oscilatório e veremos como as oscilações são utilizadas para marcar o tempo e até mesmo para medir a gravidade em determinado local.
Iniciaremos nosso estudo da ondulatória, ou seja, um estudo sobre oscilações e os diferentes tipos de ondas. Definiremos o conceito de onda e como clasificá-las quanto sua natureza e direção de propagação, assim como, apresentaremos os elementos que compõem uma onda. Nosso estudo abordará os conhecimentos relacionados desde a um simples pulso em uma corda até as ondas sonoras e eletromagnéticas. Finalmente, faremos um estudo sobre os pontos fundamentais da óptica geométrica, iniciando pelo modelo de raios luminosos, que nos permitirá desenvolver o estudo da propagação da luz e compreender a reflexão e a refração.
Em sua leitura, atente-se aos requisitos que um movimento deve atender para ser classificado como movimento harmônico simples. Busque memorizar e aplicar as funções horárias do MHS. Frequentemente a frequência angular ω é confundida com frequência f, então foque em compreender as definições e diferenças de ambas. Ao estudar o pêndulo simples, observe o período do mesmo depende apenas do comprimento do fio e da gravidade g.
Quando adentrarmos no tema da ondulatória direcione sua atenção a definição de onda e na diferença entre ondas longituninais, transversais, mecânicas e eletromagnéticas. Foque nas equações e cálculos de período, frequência e velocidade angular. Dê especial atenção a equação fundamental da onda, que é relaciona comprimento de onda, frequência e , pois é válida para todos os tipos de onda e é um dos resultados mais importantes deste tema.
Por fim, no estudo da óptica geométrica, se atente às diferenças entre imagens reais e virtuais, as leis da reflexão e aos diferentes tipos de reflexão. Quando tratarmos da refração da luz, se atente à sua lei, à lei de Snell e às condições para ocorrência de reflexão interna total, bem como ao cálculo do ângulo limite.
Nos temas a seguir, você irá aprofundar seu conhecimento com o estudo dos assuntos específicos desta unidade e, ao final, deverá atingir os seguintes objetivos de aprendizagem:
- Identificar as características de um MHS e suas aplicações.
- Descrever amplitude, frequência e período de um MHS.
- Identificar os componentes de uma onda e classificá-las.
- Descrever as características de uma imagem real e uma imagem virtual.
- Definir reflexão, refração e reflexão interna total.
Tema 1 - Fundamentos do Movimento Ondulatório
Neste tema, iniciaremos o estudo de um tipo de movimento considerado bastante especial, o movimento periódico. Quando um corpo realiza um movimento repetitivo e sempre retorna a uma mesma posição, em um intervalo de tempo fixo, temos o movimento chamado periódico. Esse movimentos repetidos dão origem as oscilações, que serão o objeto de nosso interesse.
O foco de nosso tema será em um tipo especial de movimento periódico que é chamado de Movimento Harmônico Simples (MHS), pois todos os movimentos periódicos podem ser compreendidos e modelados como um conjunto de movimentos harmônicos simples. O MHS foi chamado de especial porque fornece a base para nossa compreensão acerca de ondas mecânicas, sejam elas sonoras, sísmicas, formadas em uma corda esticada, ou ainda, formadas na água.
Quando uma onda se propaga no ar, os elementos do ar oscilam para frente e para trás, o mesmo acontece quando uma onda se propaga em um lago, seus elementos oscilam subindo e descendo. Esses movimentos oscilatórios se assemelham bastante com o movimento periódico de um pêndulo oscilatório ou de um corpo preso a uma mola.
Movimento Harmônico Simples
Um movimento é chamado periódico quando se move de forma regular, retornando a uma mesma posição após um intervalo de tempo determinado, ou seja, é um movimento que se repete em intervalos de tempos iguais.
Exemplo
O movimento periódico está aplicado em diversas situações que já observamos, uma criança em um balanço de praça, o pêndulo de um relógio ou uma corda vibrante de um violão. O movimento periódico também está presente na corrente elétrica alternada, aquela utilizada em nossas residências e na vibração dos átomos. O próprio movimento de rotação da Terra em torno do seu próprio eixo e o movimento de translação que executa em torno do sol, são exemplos de movimentos periódicos.
Em termos práticos, não basta que o corpo retorne ao seu ponto de partida, isso deve ocorrer sempre em um mesmo intervalo de tempo T. Decorrido esse intervalo de tempo, a partícula deve retornar à posição inicial com a velocidade inicial. Portanto, vale a seguinte relação para um movimento periódico:
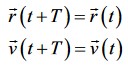
Figura 1: Relação do movimento periódico.
Fonte: Elaborada pelo autor.
Um caso especial de movimento periódico é o movimento oscilatório que pode ser definido como um movimento no qual, em algum momento, o corpo mudará de sentido. Essa inversão no sentido de movimento se dá quando a velocidade do corpo se anula e em seguida ocorre a mudança de sentido. Sendo assim, dizemos que um movimento é oscilatório se for periódico e se a mudança no sentido do movimento ocorre em intervalos de tempo iguais.
Importante
Em um movimento unidimensional, a inversão do sentido do movimento é expressa pela mudança do sinal da velocidade.
O movimento harmônico simples é um tipo particular de movimento periódico e pode ser observado em um objeto que oscila preso a uma mola. A força que a mola exerce é proporcional a elongação da mola em relação à situação de equilíbrio e é chamada de força restauradora, pois sempre aponta para a posição de equilíbrio, logo, atua no sentido contrário ao do movimento. A força elástica, dada pela lei de Hooke, é definida como:
F = - K.x
As forças de mola só têm essa dependência linear do deslocamento porque, para um sistema que está em equilíbrio, qualquer deslocamento que o retire da posição de equilíbrio fará com que a mola exerça uma força que depende linearmente do deslocamento em relação a essa posição de equilíbrio.
Temos como exemplo de movimento harmônico simples a situação de um bloco de massa m preso a uma extremidade de uma mola, livre para se mover sobre uma superfície que não tem atrito (Figura 2), que é um sistema massa-mola. Definimos a posição de equilíbrio como o ponto em que a mola não está nem alongada, nem comprimida (x = 0), em torno do qual o bloco oscila.
Para entendermos, qualitativamente, o movimento desse bloco, basta pensarmos que a força elástica sempre aponta para a posição de equilíbrio, ou seja, quando o bloco está à direita de x=0 a posição será positiva e a força elástica apontará para a esquerda, quando o bloco está à esquerda de x=0 a posição será negativa e a força elástica aponta para a direita, como mostra a Figura 2.
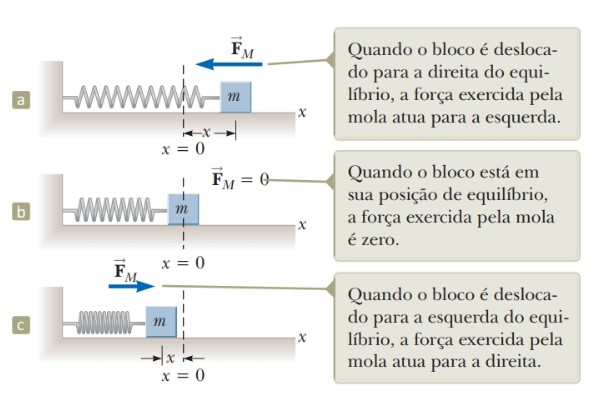
Figura 2: Sistema massa-mola em uma superfície sem atrito. Fonte: Jewett Jr.; Serway (2013, p. 3).
Outro ponto importante é que quando o bloco é afastado da posição de equilíbrio e depois liberado, passa a ser uma partícula sobre a ação de uma força resultante e como consequência sofre uma aceleração. Se aplicarmos o modelo de partícula sob a ação de uma força resultante ao nosso sistema massa-mola com a resultante Fx (na direção x), teremos:
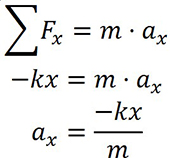
Figura 3: Modelo de partícula sob ação de uma
força resultante. Fonte: Elaborada pelo autor.
Repare que a aceleração do bloco é diretamente proporcional a sua posição e que a aceleração e o deslocamento do bloco possuem sentidos opostos, esse comportamento descreve um sistema em movimento harmônico simples.
Importante
Um corpo está em movimento harmônico simples sempre que sua aceleração for proporcional à sua posição e tiver sentido contrário ao do deslocamento a partir do equilíbrio.
Esse sistema constituído por um corpo preso a uma mola, oscilando em uma superfície lisa e horizontal, é chamado de Oscilador Harmônico Simples (Figura 3) e são duas as razões de sua grande relevância:
- A primeira é que muitos problemas que envolvem vibrações mecânicas com pequenas amplitudes podem ser reduzidos ao do oscilador harmônico simples, ou ainda, a um conjunto desses osciladores.
- A segunda é que como o oscilador harmônico simples se assemelha às características de vários sistemas físicos pode auxiliar na solução de problemas de várias áreas da física, como acústica, ótica, mecânica, circuitos elétricos e em física atômica.
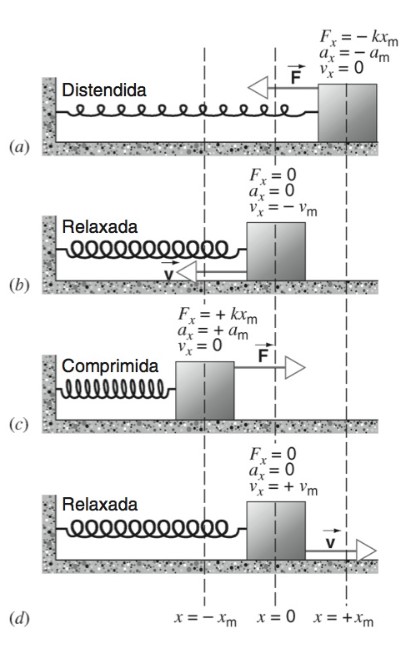
Figura 4: Oscilador harmônico simples. Fonte: Halliday;
Resnick; Krane (2017, p. 88).
Observe, na Figura 4, que, quando a mola é distendida (em a), o bloco apresenta seu deslocamento máximo em relação à posição de equilíbrio. Quando a mola é totalmente comprimida (em c) sua velocidade é zero, pois o corpo precisa parar para inverter o sentido do movimento. Nos pontos em que o bloco passa pela posição de equilíbrio (em b e d) sua velocidade é máxima e a mola se encontra relaxada. Dizemos que o bloco completa um ciclo completo de seu movimento quando retorna a sua posição original, passando novamente por x = 0 com sua velocidade máxima.
Vamos retornar à equação da aceleração a = - kx/m e lembrar que a aceleração é fornecida pela segunda derivada da posição, o que nos leva a:
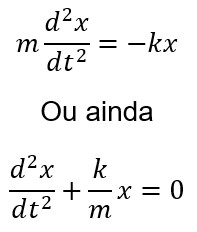
A parcela K/m é representada por ω2, sendo assim

O que nos leva à equação:
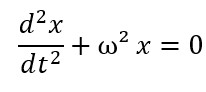
A descrição matemática do movimento harmônico simples será dada pela solução dessa equação diferencial. Vamos encontrar uma função x(t) que satisfaça a nossa equação diferencial de segunda ordem e que, ao mesmo tempo, represente matematicamente a posição da partícula em função do tempo.
Para isso precisaremos chegar a uma função que tenha como segunda derivada a mesma que a função original com um sinal negativo e multiplicada por ω2. Para isso, precisaremos de uma função seno ou cosseno, pois apresentam esse comportamento que estamos buscando. Criando uma solução a partir da função cosseno, temos:
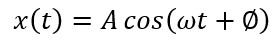
Essa é a equação da posição para uma partícula em movimento harmônico simples, também chamada de função horária da posição. Onde A, ω e Ø são constantes. A quantidade A é chamada de amplitude e ω é a frequência angular (ou velocidade angular), dada por $\omega=\sqrt{\frac km}$ e que será expressa em rad/s (radianos por segundo), tanto a amplitude quanto a velocidade angular são constantes.
A amplitude do movimento A pode ser compreendida, simplesmente, como o valor máximo da posição da partícula atingida na direção x (Figura 5), positiva ou negativa. Enquanto a frequência angular ω, que é constante, mede quão rapidamente as oscilações acontecem; ou seja, quanto mais oscilações por unidade de tempo, maior será o valor de ω.
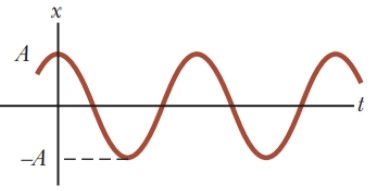
Figura 5: Gráfico do MHS de uma partícula evidenciando a amplitude A.
Fonte: Jewett Jr.; Serway
(2013, p. 5).
O ângulo Ø também é constante e é chamado de constante de fase, ou ângulo de fase inicial, sendo determinado, juntamente com A, pela posição e pela velocidade em t=0. Quando a partícula se encontrar em sua máxima posição x = A em t =0, a constante de fase será Ø = 0 e o movimento será representado pela Figura 6.
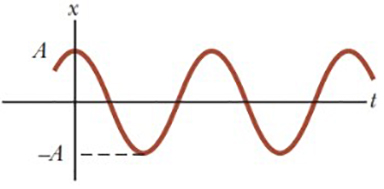
Figura 6: Gráfico da Posição vs. Tempo para uma partícula em MHS.
Fonte: Jewett Jr.; Serway (2013,
p. 5).
Analisando o gráfico de posição versus tempo, identificamos as características do MHS. A seguir, aplicaremos esses conceitos em um exemplo concreto.
Exemplo
A posição de uma partícula em MHS é dada pela seguinte equação horária:
$\mathrm x\;=\;5\;\cos\;(2\mathrm{πt}\;+\frac{\mathrm\pi}4)$. Determine a amplitude, a frequência angular e o ângulo de fase, em unidades do SI.
Para determinar esses elementos precisamos comparar a função horária dessa partícula com a função horária do MHS
x(t) = A cos (ωt + Ø)
Podemos observar que a amplitude é o valor que multiplica o cosseno, a frequência angular se multiplica com o tempo t e o angulo de fase é o termo que aparece sozinho, somando-se ao termo ωt. Sendo assim,
A = 5m
ω = 2π rad/s

As derivadas, primeira e segunda, da equação da posição, resultam nas equações para a velocidade e aceleração de uma partícula em movimento harmônico simples, dadas, respectivamente, por:
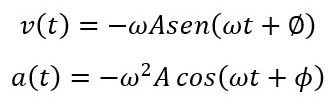
Essas equações são chamadas de função horária da velocidade do MHS e função horária da aceleração do MHS, respectivamente.
Sabemos que as funções seno e cosseno oscilam entre ±1, então os valores extremos da velocidade v são ± ωA e os valores extremos da aceleração a são ± ω2A. Sendo assim, temos que os valores máximos dos módulos da velocidade e aceleração, que são:

O gráfico abaixo, Figura 7, esboça a posição versus tempo a partir de um valor arbitrário para a constante de fase e as curvas de velocidade x tempo, e aceleração x tempo associadas estão ilustradas nas Figuras 7b e 7a, respectivamente. Podemos observar que a fase da velocidade é diferente da fase da posição.
Essa diferença, que é de π/2 radianos, ocorre porque quando x é um máximo ou mínimo (amplitudes máximas) a velocidade é zero e quando x é zero a velocidade é máxima. Já a fase da aceleração difere da fase da posição por π radianos, ou seja, quando x for máximo, a aceleração a será máxima, em módulo, e apontará para a direção oposta.
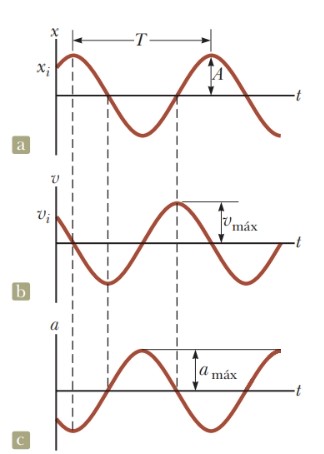
Figura 7: Gráficos de Posição x Tempo, Velocidade x Tempo e
Aceleração x Tempo para o MHS. Fonte:
Jewett
Jr.; Serway (2013, p. 6).
Os gráficos acima ilustram a relação entre posição, velocidade e aceleração no MHS. Vamos analisar um exemplo para visualizar essas relações em um caso específico.
Exemplo
Um bloco de 200g oscila, preso a extremidade de uma mola de constante k=5N/m, em uma superfície lisa e horizontal. Sabendo que o bloco foi deslocado de 0,05m em relação à posição de equilíbrio e liberado do repouso, encontre a frequência angular ω do sistema bloco-mola, uma expressão para x(t) e calcule a velocidade e a aceleração máximas.
Vamos calcular a frequência angular, lembrando de converter a massa para quilogramas:

Já calculamos ω e, de acordo com o enunciado, A=0,05m. Escrevendo uma expressão para x(t), partindo de $x(t)=A\;cos(\omega+\varnothing)$ temos que:

Por fim, calculando vmáx e amáx


Figura 8: Ponte do Milênio, em Londres. Fonte: Dreamstime.
A Ponte do Milênio, sobre o Rio Tamisa, em Londres. No dia da abertura da ponte, os pedestres observaram um movimento oscilante da ponte, levando a ser chamada de “Ponte Trêmula”. A ponte foi fechada após dois dias e permaneceu fechada por dois anos. Mais de 50 amortecedores foram adicionados à ponte: pares massa-mola localizados sobre os apoios da estrutura (Jewett Jr.; Serway, 2013).
Período e Frequência
Para aprofundar um pouco mais o movimento harmônico simples, vamos considerar uma grandeza chamada período, representada pela letra T maiúscula.
O período T de um movimento é o intervalo de tempo necessário para que a partícula execute uma oscilação completa, ou um ciclo completo de seu movimento. Por exemplo, a rotação da Terra tem um período de 24h, ou seja, a cada 24h a Terra completa um ciclo, retornando à posição inicial.
O período é fornecido pela seguinte equação:
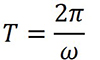
A frequência, que é o inverso do período, fornece a quantidade de oscilações que a partícula executa por unidade de tempo, sendo expressa da seguinte forma:

Ou, ainda,

Também é possível escrever a frequência em função da frequência angular:

A frequência pode ser dada pelas seguintes unidades: ciclos por segundo ou hertz (Hz).
Importante
Não confunda a frequência f com frequência angular ω, a frequência angular é uma medida de velocidade e difere da frequência f por um fator igual a 2π.
Observando as equações abaixo, percebe-se que o período e a frequência dependem apenas da massa da partícula e da constante elástica da mola K, e não de parâmetros do movimento, como é o caso da amplitude e do ângulo de fase Ø. A frequência será maior para molas que são mais rígidas, ou seja, que possuem um valor de constante elástica K maior. A frequência é inversamente proporcional à massa da partícula, logo, diminui com o aumento da massa.
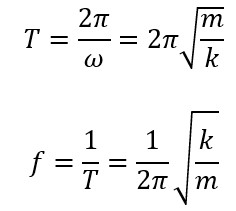
Exemplo
Um bloco de massa m = 0,5 Kg está preso a uma mola de constante elástica k = 200 N/m. Após esticar a mola o corpo é liberado do repouso e executa um MHS. Determine o período e a frequência do movimento.
Primeiramente, é necessário que calculemos a frequência angular ω:

Aplicando a equação do período, temos:

Para calcular a frequência, basta lembrar que ela é o inverso do período:

Um outro modo de calcular a frequência é a partir de sua relação com a frequência angular ω:

Curiosidade
O menor relógio atômico do mundo, do Nacional Institute of Standards and Technology (Instituto Nacional de Padrões e Tecnologia dos Estados Unidos), no qual átomos de césio efetuam 9,2 bilhões de oscilações por segundo. O relógio é do tamanho de um grão de arroz e sua precisão é de 1 parte em 10 bilhões – o que equivale a um erro de menos de 1 s em um período de funcionamento de 300 anos (Bauer; Westfall; Dias, 2012).
Compreender o período e a frequência é fundamental para analisar qualquer sistema que oscila em MHS. Com esses conceitos, podemos prever o comportamento do sistema ao longo do tempo.
Pêndulo Simples – Uma Aplicação do MHS
O pêndulo simples consiste em uma massa suspensa, presa a um fio inextensível de comprimento L fixada em uma extremidade superior, conforme ilustra a Figura 9. Esse sistema mecânico exibe um movimento harmônico simples e é movido pela força gravitacional. Para um angulo θ bem pequeno, menor que 10°, aproximadamente, o movimento do pêndulo é muito semelhante ao do oscilador harmônico simples.
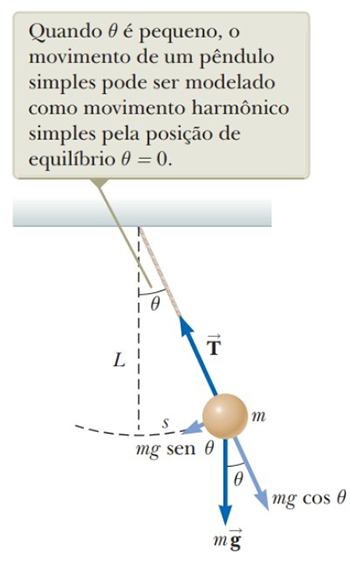
Figura 9: Pêndulo simples. Fonte: Jewett Jr.; Serway (2013, p. 15).
As forças que atuam sobre a massa m são a tração T, exercida pelo fio e a força peso, chamada gravitacional m.g. Como o movimento do pêndulo simples para pequenas amplitudes de oscilação pode ser modelado como MHS, temos como resultado as seguintes equações para a frequência angular e período do movimento pendular, respectivamente.

O período do movimento é:

Onde g é o valor da gravidade no local e L é o comprimento do fio.
Observe que o período e a frequência de um pêndulo simples dependem apenas do comprimento do cordão e da gravidade.
Importante
O período é independente da massa e a consequência disso é que todos os pêndulos simples que tenham o mesmo comprimento e que estejam sujeitos a mesma gravidade, ou seja, estejam em um mesmo local, oscilarão com o mesmo período.
Umas das aplicações do pêndulo simples é utilizá-lo como um marcador de tempo, já que seu período depende somente de seu comprimento e do valor da gravidade local.
Curiosidade
O pêndulo simples também é um aparelho conveniente para fazer medições precisas da aceleração da gravidade, o que é de suma importância, pois variações nos valores locais de g podem ser úteis para fornecer informações sobre localização de óleo e outros recursos subterrâneos de bastante valor.
Com o pêndulo simples, vimos uma aplicação prática do MHS. A partir daqui, podemos explorar outros sistemas oscilatórios mais complexos.
Neste tema, estudamos os movimentos periódicos, aqueles que se repetem em intervalos de tempo iguais e sucessivos, em outras palavras, um movimento é periódico se, após decorrido um intervalo de tempo fixo, o ponto material se encontra na mesma posição inicial e com a mesma velocidade. Destacamos entre os movimentos periódicos o movimento harmônico simples, que nessa classe de movimentos é o mais simples de todos.
O movimento harmônico simples é ao mesmo tempo um movimento periódico e oscilatório, já que de tempos em tempos ocorre uma inversão no sentido do movimento. Vimos que para um movimento ser classificado como MHS é necessário que satisfaça algumas condições, esse movimento deve acontecer devido a ação de uma força de comportamento elástico, que obedece a lei de Hooke e deve ser oscilatório. O MHS possui um período, que é o tempo gasto para completar uma oscilação e uma frequência, que fornece o número de oscilações que ocorrem em um intervalo de tempo. Por fim, vimos que o pêndulo simples é uma aplicação prática do MHS, já que pode ser modelado como MHS.
Tema 2 - Ondas Sonoras e Eletromagnéticas
Neste tema, iniciaremos nosso estudo sobre o movimento ondulatório. Certamente muitos de nós já teve a experiência de arremessar uma pedra na água de um lago e observar a formação de ondas circulares no ponto onde a pedra caiu. Essas ondas vão se expandindo até atingirem a margem.
Exemplo
Se desejássemos fazer uma análise um pouco mais detalhada desse fenômeno, bastaria colocar um objeto, uma rolha de cortiça, por exemplo, na água perturbada. Seria possível notar que a rolha faria um movimento de sobe e desce e também na horizontal, em relação a sua posição inicial, mas nenhum deslocamento efetivo aconteceria em relação ao ponto onde a pedra atingiu a água. Isso ocorre porque a onda na água se move do seu ponto de origem até a margem, mas não carrega água com ela.
As ondas vão muito além de uma perturbação na água, o som e a luz são exemplos de ondas e o movimento ondulatório se faz presente em terremotos, tsunamis, transmissões de rádio e de televisão. As partículas mais fundamentais da matéria apresentam propriedades semelhantes as das ondas e podemos dizer que até mesmo nós somos feitos de ondas e partículas, em certo sentido.
Movimento Ondulatório
Até aqui, nosso estudo se baseou em sistemas macroscópicos, formados por moléculas, que podem ser considerados como uma partícula ou um sistema formado por elas. Existem dois modelos fundamentais para a física clássica, o primeiro é o de partículas, e o segundo, para o qual nos voltaremos agora, é o modelo de onda. As ondas sonoras e luminosas nos são bastante familiares e estão vinculadas a nossa percepção de ambiente, já que seres humanos possuem olhos e ouvidos, que são receptores capazes de detectar essas ondas.
Vamos examinar o comportamento e as propriedades das ondas, utilizando os conhecimentos vistos no tema anterior, sobre oscilações.
Exemplo
O estudo da ondulatória compõem áreas inteiras da física, como a óptica e acústica, por exemplo, mas também é fundamental para a astronomia e eletrônica.
Então, daremos início a um estudo que nos dará a oportunidade de compreender uma grande parte desse vasto mundo físico ao nosso redor. O movimento ondulatório como uma transferência de energia através do espaço sem que haja transporte de matéria.
Ao fixar uma corda na parede, segurar a outra extremidade e movê-la rapidamente para baixo e para cima, a crista de uma onda se formará e se propagará através da corda (Figura 10). Apesar de a onda se mover por meio do material, fazendo-o subir e descer, a corda permanece no mesmo lugar. Esse exemplo nos ajuda a compreender uma das principais características das ondas, explicitando que uma onda é uma perturbação que se propaga pelo espaço, ou através de um meio, em função do tempo, mas sem transportar matéria consigo.
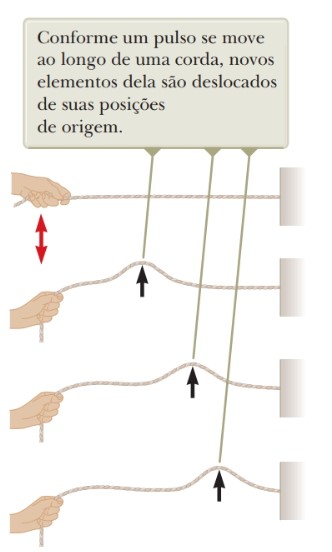
Figura 10: Mão Move extremidade de uma corda esticada formando
um pulso. Fonte: Jewett Jr.; Serway
(2013, p. 35).
O modelo ondulatório é baseado na ideia de onda progressiva, um tipo de perturbação organizada e que se movimenta com uma velocidade de onda bem definida. Uma onda pode se mover de duas maneiras distintas e serão classificadas de acordo com esses movimentos.
Uma onda transversal é aquela onde os deslocamentos que ocorrem no meio de propagação são perpendiculares ao sentido de propagação da onda. Por exemplo, em uma onda que se propaga em uma corda esticada, vemos que os elementos da corda se movem verticalmente, enquanto a onda se move na horizontal, como ilustra a Figura 11.
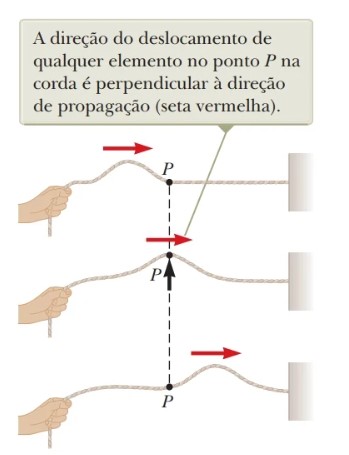
Figura 11: Deslocamento de um elemento específico da corda por um pulso transversal
ao longo de uma
corda esticada. Fonte: Jewett Jr.; Serway (2013, p. 35).
Uma onda é dita longitudinal quando os elementos do meio se movimentam paralelamente ao sentido de propagação da onda, como o caso de um pulso se propagando em uma mola, como mostrado na Figura 12.
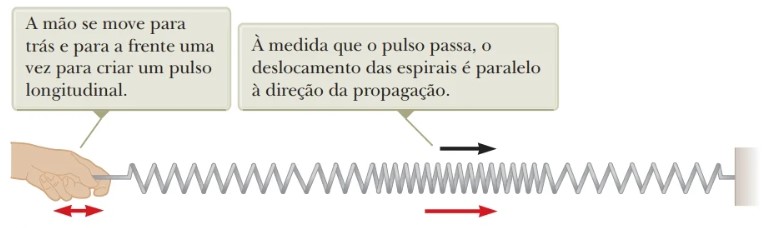
Figura 12: Onda longitudinal se movendo em uma corda esticada. Fonte: Jewett Jr.; Serway (2013, p. 35).
Demonstramos as características das ondas, desde sua natureza ondulatória até a forma transversal de propagação. Que tal uma pausa para uma curiosidade sobre o tema?
Curiosidade
As ondas que se propagam na água possuem características tanto de ondas longitudinais quanto de ondas transversais. A superfície da água se move na vertical, para cima e para baixo, mais os elementos individuais da água se movem perpendicular e longitudinalmente ao sentido de propagação da onda.
As ondas também podem ser classificadas quanto à sua natureza:
- Ondas mecânicas: são ondas que necessitam de um meio material para se propagarem, o ar ou a água, por exemplo. São exemplos comuns de ondas mecânicas, as ondas na água e as ondas sonoras.
- Ondas eletromagnéticas: são ondas que não necessitam de um meio material para se para se propagarem, podem propagar-se no vácuo. A luz, os raios-x e radiação gama são exemplos de ondas eletromagnéticas.
- Ondas de matéria: são a base da física quântica. No século XX foi descoberto que partículas de matéria, como os elétrons, por exemplo, exibem comportamento ondulatório.
As ondas transversais, com sua oscilação perpendicular à propagação, são fascinantes! Com esse conhecimento, podemos avançar para outros tipos de ondas e fenômenos ondulatórios.
Ondas Senoidais
Temos a geração de uma onda senoidal quando a fonte emissora da onda oscila em movimento harmônico simples (MHS). Um cone de alto-falante, por exemplo, oscila em MHS e por consequência gera uma onda sonora senoidal, enquanto as estações de rádio FM e de televisão, fruto da oscilação de elétrons em MHS, são ondas eletromagnéticas senoidais.
Importante
A frequência da onda gerada é sempre igual à frequência da fonte de oscilação.
Podemos ver, ilustrado na Figura 13, uma onda senoidal se movendo em um meio material e a fonte que está gerando essa onda se localiza em x=0. É possível notar que as cristas das ondas se movem com velocidade constante rumo a valores maiores de x em instantes posteriores t.
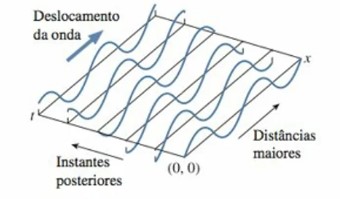
Figura 13: Onda senoidal de propagamento ao
longo de x. Fonte: Knight (2009, p. 189).
A seguir, vamos desenvolver os elementos que compõem uma onda e as principais relações matemáticas para representá-la. Do mesmo modo que aprendemos a calcular o período do MHS no tema anterior, faremos para calcular o período de uma onda. O período de uma onda é o intervalo de tempo gasto para completar um ciclo do movimento e dado pelo inverso da frequência da onda:

A Figura 14 apresenta o gráfico-história de uma onda senoidal, evidenciando o deslocamento do meio material em uma determinada região do espaço, onde cada elemento do meio realiza MHS de frequência f. Na parte b da Figura 14, vemos a mesma onda em um certo instante do tempo, se movendo para a direita com velocidade v. Quanto aos elementos da onda (Figura 14b), a amplitude A é definida como o maior valor atingido pelo deslocamento da onda. O ponto mais alto da onda, chamado crista tem amplitude A e a parte mais baixa, chamada vale, tem amplitude –A. Vale ressaltar que toda onda senoidal é periódica tanto no espaço quanto no tempo.
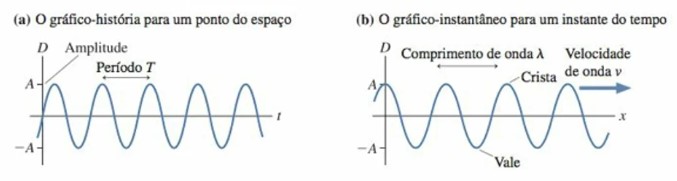
Figura 14: Gráfico-história para um ponto do espaço (a) e gráfico-instantâneo para a mesma onda
em
um dado instante de tempo (b). Fonte: Knight (2009, p. 189).
Chamamos de comprimento de onda λ a distância que corresponde a um ciclo completo da onda e é dado em metros. O comprimento de onda também pode ser dado pela distância entre duas cristas ou dois vales, consecutivos.
Importante
“O comprimento de onda é o análogo espacial do período. O período T é o tempo durante o qual a perturbação se repete em cada ponto do espaço. O comprimento de onda é a distância na qual a perturbação se repete para cada instante de tempo.” (Knight, 2009, p. 190)
Considerando a relação que há entre o comprimento de onda e o período de oscilação, ou seja, que decorrido um intervalo de tempo correspondente a um período T, a crista de uma onda terá se deslocado, exatamente, de um comprimento de onda λ, chegamos à equação fundamental de onda
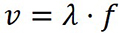
Onde v é a velocidade da onda, que é uma propriedade do meio. Já a frequência f é uma propriedade da fonte.
Exemplo
Uma onda senoidal progressiva propaga-se no sentido positivo de x com comprimento de onda de 80 cm e frequência de 10 Hz. Calcule a velocidade de propagação dessa onda.
Primeiramente, vamos ajustar a unidade de medida do comprimento de onda para metros λ = 80 cm /100 = 0,8 m. Aplicando a equação fundamental de onda, temos:

A onda se propaga com velocidade igual a 8 m/s.
No tema anterior, no qual estudamos o MHS, definimos uma função x(t) que nos fornecia o deslocamento de uma partícula do meio em função da posição x e do tempo t. De forma análoga, há uma função de deslocamento (que fornece o deslocamento vertical de um elemento do meio) para o caso de uma onda senoidal, na forma compacta, é dada por:
Y (x,t) = A sen (kx - ωt)
Essa função também é chamada de função ondular para uma onda senoidal, onde A é a amplitude da onda, ou seja, é a posição máxima que um elemento de um meio atinge em relação a sua posição de equilíbrio e ω é a frequência angular. Note que introduzimos uma nova quantidade k chamada de número de onda, dado por
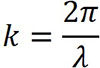
A função ondular para uma onda senoidal evidencia a natureza periódica de Y, pois em dado instante t, y tem o mesmo valor que as posições x, x + λ, x + 2 λ, em outros termos, a posição vertical Y é a mesma sempre que x é aumentado por um múltiplo inteiro de λ.
Do mesmo modo que no movimento harmônico simples, a constante de fase Ø, ou angulo de fase, caracteriza as condições iniciais. Se temos valores diferentes de Ø, então as condições iniciais são diferentes para a onda. Logo, a função senoidal ainda pode ser escrita como:
Y (x,t) = A sen (kx - ωt + Ø)
Exemplo
Sabe-se que uma onda senoidal progressiva está se propagando na direção positiva de x com amplitude de 0,2m, comprimento de onda de 0,4m e frequência de 8,0 Hz. A posição vertical do elemento no meio em t = 0 e x = 0 também é de 0,2m. Determine a frequência angular, o número de onda, o período, a velocidade e escreva uma expressão geral para a função ondular.
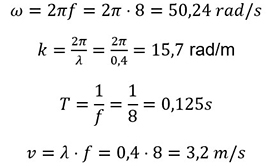
Substituindo A = 0,2 m e Y = 0,2 m, x=0 e t =0 na equação Y (x,t) = A sen (kx - ωt + Ø), temos:
0,2 = 0,2 . sen (Ø)
sen (Ø) = 1

Logo, Y = 0,20 sen (15,7x – 50,24t + π/2)
Ondas senoidais: a chave para desvendar o mundo das ondas. Prossiga sua jornada pelo universo ondulatório!
Ondas Sonoras e Ondas Eletromagnéticas
Vamos voltar nossa atenção para as sonoras, que podem se propagar em qualquer meio material.
Observe a Figura 15, que ilustra uma onda contínua de pressão com variações na pressão do ar. Ora tem-se um excesso de pressão, chamado de compressão, ora tem-se uma redução de pressão, chamada de rarefação. Ao registramos essas variações ao longo do eixo x e os instantes correspondentes podemos obter a velocidade da onda sonora.
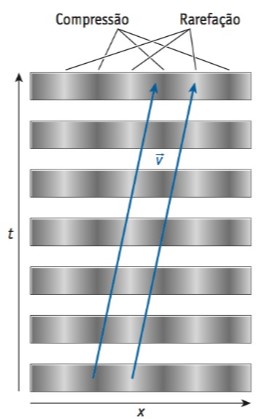
Figura 15: Onda longitudinal de pressão ao longo do eixo x
em função do tempo t. Fonte: Bauer;
Westfall;
Dias (2012, p. 135).
As ondas sonoras se dividem em três classes de acordo com a faixa de frequência que atingem.
- As ondas que se encontram dentro da faixa de frequência perceptível ao ouvido humano são chamadas de ondas audíveis. O ouvido humano consegue detectar sons com frequências entre 20 Hz e 20.000 kHz. Essas ondas podem ser geradas de formas distintas, por um alto-falante, cordas de um violão ou pela voz, por exemplo.
- As ondas que possuem frequência abaixo das ondas audíveis são chamadas de infrassons. Animais como os elefantes, por exemplo, utilizam infrassons para se comunicarem.
- Já as ondas de ultrassom possuem frequência acima da faixa audível. Os apitos silenciosos utilizados para chamar cães emitem ultrassons, que são ouvidos por esses animais. As ondas de ultrassom são comumente utilizadas em exames médicos.
Durante uma tempestade, quando vemos um raio “cortar” o céu, primeiramente enxergamos sua luz e depois ouvimos seu som. Isso ocorre, pois a luz emitida pelo raio atinge nossos olhos quase instantaneamente, já que a velocidade da luz é de aproximadamente 3.108m/s.
Curiosidade
O som possui velocidade muito menor que a da luz, de modo que o som chega aos nossos ouvidos algum tempo depois de vermos a luz.
O som pode propagar em sólidos, líquidos ou gases, apresentando velocidades diferentes de acordo com o módulo de Young do material, de modo que, vale a seguinte relação para a propagação do som em sólidos, líquidos e gases:
Vsólido > Vlíquido> Vgás
Entretanto, o que mais nos interessa é a velocidade do som no ar, pois é o meio material mais importante quanto a propagação do som em nosso cotidiano. A velocidade do som, à pressão atmosférica normal e a 20°C, vale, aproximadamente
Vsom ar = 343 m/s
Curiosidade
O conhecimento do valor da velocidade do som no ar explica a regra dos 5 s para relâmpagos: se 5 s ou menos transcorrem entre o instante em que se vê̂ um raio e o instante em que se escuta o correspondente trovão, é porque o raio caiu a cerca de 1,6 Km de distância ou menos. Sabendo que a velocidade do som é de aproximadamente 340 m/s, ele se desloca 1.700 m em 5 s. A velocidade da luz é de cerca de 1 milhão de vezes maior do que a do som, de modo que a percepção visual do raio ocorre basicamente sem retardo (Bauer; Westfall; Dias, 2012).
As ondas sonoras podem ser refletidas, como o caso do eco, por exemplo.
O fenômeno da reflexão de ondas sonoras nos permite determinar a distância até́ um objeto medindo-se o tempo entre a emissão do som e o momento em que se ouve o som novamente, após atingir um anteparo e ser refletido por ele.
A reflexão do som ocorre quando a onda sonora atinge um obstáculo, é refletida por ele e retorna ao meio de origem da propagação. Para calcular a distância entre um objeto e a fonte emissora da onda, basta conhecer a velocidade do som no meio de propagação e utilizar a equação:
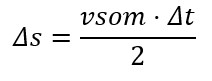
Onde vsom é a velocidade do som no meio de propagação. Note que a quantidade vsom.∆t está dividida por 2, isso se deve ao fato de, na reflexão, o som percorrer a distância duas vezes, na ida e na volta, quando reflete. É exatamente esse o princípio utilizado no mapeamento com ultrassom para finalidades médicas.
As ondas eletromagnéticas incluem a luz, os raios-x, os raios-γ, ondas de rádio e micro-ondas, por exemplo. Essas ondas irão diferir entre si apenas pela frequência e comprimento de onda. Como vimos, as ondas mecânicas necessitam de um meio para se propagarem, mas as ondas eletromagnéticas não, elas se propagam no vácuo com uma velocidade constante c = 3.108 m/s. As ondas eletromagnéticas resultam de um campo elétrico e um campo magnético oscilantes e perpendiculares entre si, como mostra a Figura 16, sendo assim, essas ondas são transversais.
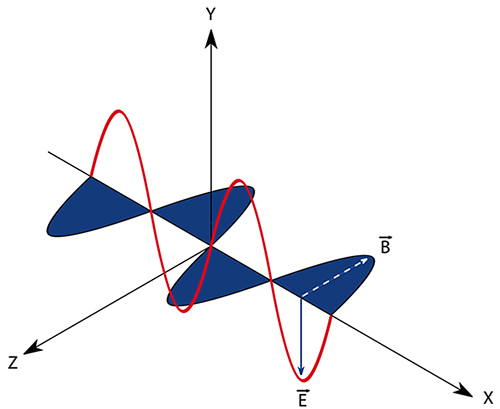
Figura 16: Onda eletromagnética. Fonte: Dreamstime.
O espectro eletromagnético, Figura 17, mostra as ondas eletromagnéticas de comprimentos de onda na faixa de 1.000 m a menos do que 10–12 m, e respectivas frequências de 105 a 1020 Hz. As ondas eletromagnéticas recebem nomes específicos de acordo com a faixa de frequência em que se enquadram.
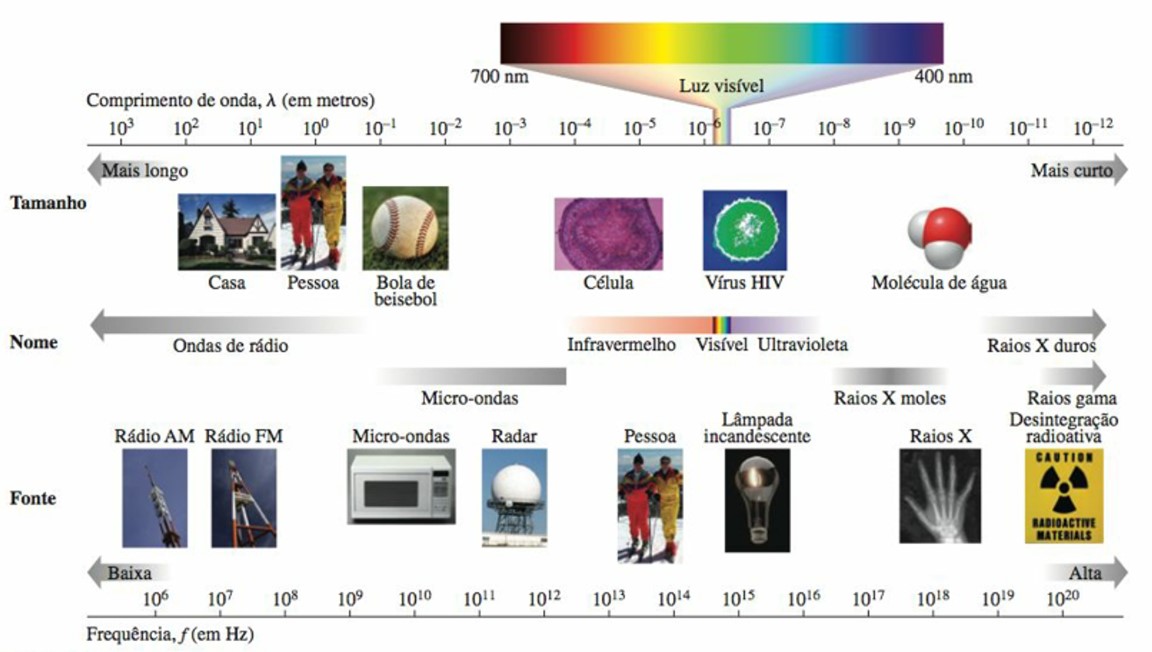
Figura 17: Espectro eletromagnético. Fonte: Bauer; Westfall; Dias (2012, p. 345).
Note que as ondas eletromagnéticas que estão na faixa da luz visível correspondem apenas a uma pequena parcela de todas as radiações eletromagnéticas conhecidas. A luz visível possui comprimentos de onda entre 400nm e 700nm, ou seja, entre 4.10-7m e 7.10-7m e sua frequência é da ordem de 1014 Hz.
Neste tema, estudamos o que é o movimento ondulatório, aquele realizado pelas ondas e que consiste em um transporte de energia que não carrega matéria consigo. Definimos onda como uma perturbação que se propaga no espaço ou em um meio material e classificamos as ondas como longituniais quando a direção de propagação coincide com a de vibração e como transversais quando a direção de vibração e de propagação são perpendiculares. Vimos que quando a fonte que emite uma onda oscila em movimento harmônico simples gera uma onda chamada senoidal, que é periódica e possui um período, uma frequência e frequência angular associados a ela.
Descrevemos os elementos que compõem uma onda, seu período, que é o tempo gasto para que se complete uma oscilação e o seu análogo espacial, que é o comprimento de onda, que é a distância na qual a perturbação se repete para cada instante de tempo. Vimos que o ponto mais alto e mais baixo de amplitude, é chamado, respectivamente, de crista e vale. Feito isso, deduzimos uma relação importantíssima para a ondulatória, a equação fundamental de onda, que vale para qualquer tipo de onda e nos permite encontrar a velocidade de propagação a partir da frequência e do comprimento de onda. Por fim, aprofundamos os conhecimentos acerca do som, uma onda mecânica que necessita de um meio para de propagar e acerca de ondas eletromagnéticas, que se propagam no vácuo com velocidade c = 3.108 m/s, a velocidade limite no universo.
Tema 3 - Fundamentos de Óptica Geométrica
A óptica é um estudo da luz e pode ser divido em três partes:
- óptica geométrica;
- óptica ondulatória;
- óptica quântica.
Nosso estudo se baseará na óptica geométrica e, embora já tenhamos visto que a luz é uma onda eletromagnética, trataremos dos fenômenos luminosos a partir do modelo de raio luminoso, ou seja, vamos ignorar o caráter ondulatório da luz para compreender situações em que o sistema apresenta dimensões muito maiores que o comprimento de onda da luz. Vamos considerar apenas como a luz se propaga pelo ar, vidro, água ou outro tipo de meio.
O modelo de raio de luz pode ser uma simplificação exagerada da realidade, mas é muito conveniente, já que a nossa experiência cotidiana nos revela que a luz se propaga em linha reta. Já vimos a luz de uma lanterna emitindo um feixe luminoso em um ambiente escuro, ou ainda, os raios de sol passando pelo orifício de uma persiana e tornando-se evidentes em um quarto escuro. Apesar do modelo de raio luminoso parecer simplório, a óptica geométrica (por vezes chamada de óptica de raio) tem um grande valor prático, pois permite a análise de sistemas ópticos básicos, como as lentes e espelhos.
O Modelo de Raios Luminosos
Vamos começar definindo que um raio luminoso é uma representação da luz, em forma de linha reta e que ilustra a direção e o sentido de propagação da luz. O modelo de raio de luz é um recurso abstrato, não é uma entidade ou uma grandeza física. Uma outra definição necessária para nosso estudo é a de feixe de luz, que é um conjunto formado por vários raios luminosos, conforme ilustrado na Figura 18.
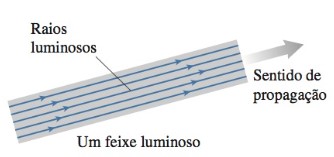
Figura 18: Feixe luminoso. Fonte: Knight (2009, p. 282).
O modelo de raios luminosos engloba alguns princípios:
Há ainda algumas informações relevantes acerca do modelo de raio luminoso, por exemplo, um raio de luz continua se propagando, indefinidamente, exceto, se sofrer alguma interação com a matéria. A interação da luz com a matéria pode acontecer de quatro formas: Reflexão, refração, espalhamento ou absorção.
Todo objeto é uma fonte de raios luminosos, raios estes que se originam de todos os pontos do objeto e que se propagam em todas as direções.
Exemplo
Vale ressaltar, que alguns objetos possuem luz própria, como o sol e outros são apenas refletores, uma árvore.
Quando os raios luminosos provenientes dos objetos atingem a pupila do olho humano, uma imagem do objeto é formada sobre a retina e o cérebro “calcula” a distância na qual esses raios se originam e assim enxergamos os objetos e onde se localizam. Em outras palavras, um objeto que não possui luz própria só pode ser visto se refletir a luz proveniente de alguma fonte luminosa. A Figura 19 ilustra uma árvore refletindo a luz que recebe do sol, ou seja, objetos refletores e objetos que emitem luz própria.
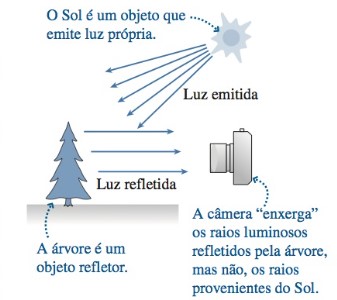
Figura 19: Objetos refletores e os de luz própria. Fonte: Knight (2009, p. 282).
Como visto, os raios de luz se originam de todos os pontos do objeto, mas para fins didáticos, utilizaremos um recurso chamado de diagrama de raios, que mostra apenas os raios que são emitidos dos pontos superiores e inferiores do objeto.
Exemplo
Um exemplo de aplicação de diagrama de raio é a câmara escura, que consiste em uma caixa de paredes internas escuras e opacas com um pequeno orifício para entrada da luz. Quando um objeto é colocado em frente à câmara, uma imagem do objeto é formada na parede oposta. Mesmo que um objeto emita raios luminosos em todas as direções e sentidos, apenas alguns poucos raios passam pela abertura e atingem a parede traseira, gerando uma imagem de cabeça para baixo.
Confira isso na Figura 20.
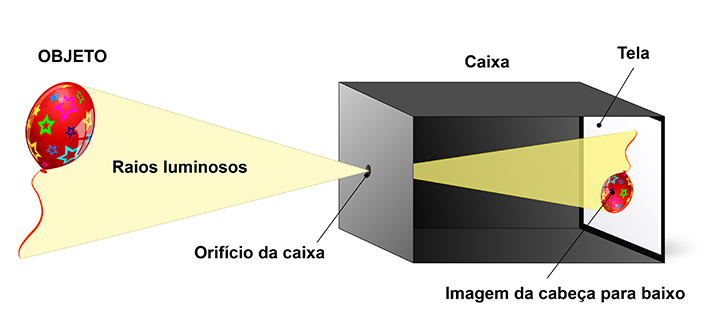
Figura 20: Câmara escura. Fonte: Adaptada de Dreamstime.
A partir da semelhança dos triângulos, é possível verificar que a altura do objeto e da imagem formada estão relacionadas por:
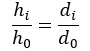
Onde di é a distância do orifício à imagem, do é a distância do objeto ao orifício, ho é a altura do objeto e hi é a altura da imagem.
Exemplo
Uma lâmpada de 10 cm de altura é posta a 50 cm de uma câmara escura, como ilustra a figura. Sabendo que a distância entre o orifício da câmara e a imagem formada é de 30 cm, qual a altura da imagem formada?
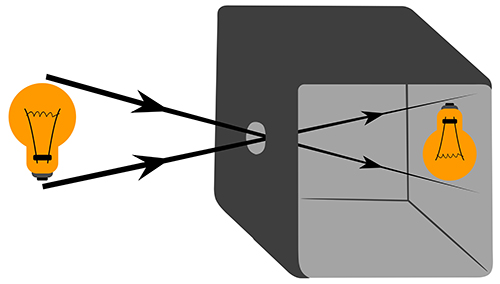
Figura 21: Lâmpada frente a uma câmara escura, ao projetar sua imagem invertida.
Fonte: Dreamstime.
Agora, vamos organizar os dados para depois substituir na equação de semelhança dos triângulos
- di = 30 cm
- do = 50 cm
- ho = 10 cm
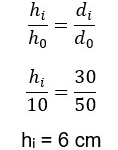
A imagem formada na parede da câmera tem 6 cm de altura.
Compreender o comportamento da luz como raios facilita o estudo de lentes e espelhos. A óptica geométrica se torna mais acessível com essa ferramenta.
A Reflexão e a Refração da Luz
A reflexão da luz, provavelmente, é o fenômeno mais comum envolvendo a propagação da luz. Lidamos com a reflexão a todo instante enquanto enxergamos os objetos, quando vemos nossa imagem em um espelho.
Dizemos que houve reflexão quando a luz incide sobre uma superfície que faz separação entre dois meios com propriedades distintas e volta ao meio de propagação de origem.
Quando a reflexão ocorre em uma superfície lisa e regular é chamada de reflexão especular (ou regular), onde raios incidentes paralelos terão raios refletidos correspondentes também paralelos. Se a superfície refletora for irregular, mesmo que os raios incidentes sejam paralelos, serão refletidos em direções aleatórias, conforme vemos na Figura 22.
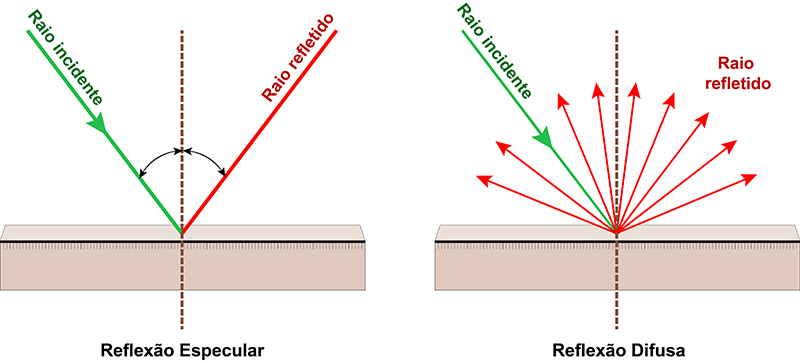
Figura 22: Reflexão especular e reflexão difusa. Fonte: Adaptada de Dreamstime.
Em resumo, a reflexão da luz é quando a luz retorna ao meio de origem após incidir em uma superfície. Superfícies lisas geram reflexão regular (imagens nítidas), enquanto superfícies irregulares causam reflexão difusa (luz espalhada).
Importante
Uma superfície é chamada irregular quando possui texturas, arranhões, irregularidades em comparação ao comprimento de onda da luz emitida. Como a luz visível tem comprimentos de onda na faixa de 5μm, superfícies com irregularidades maiores que 1μm provocarão reflexão difusa. Os espelhos planos possuem irregularidades muito menores que 1μm e por isso provocam reflexão especular.
Vejamos algumas observações essenciais: Para que as figuras fiquem claras e a análise seja mais fácil, adotaremos um único raio luminoso para representar todo o feixe de raios paralelos. Chamaremos de reta normal N a reta imaginária, perpendicular à superfície refletora (forma um angulo de 90° com a superfície refletora), de ângulo de incidência θi o angulo formado entre o raio incidente e a reta normal e de ângulo de reflexão θr o angulo formado entre o raio refletido e a normal (Figura 23).
O fenômeno da reflexão da luz é descrito por duas leis que podem ser, facilmente, demonstradas com experimentos simples.
1ª Lei da Reflexão: o raio incidente, a reta normal e o raio refletido pertencem ao mesmo plano.
2ª Lei da Reflexão: o angulo de incidência é igual ao angulo de reflexão: θi = θr.
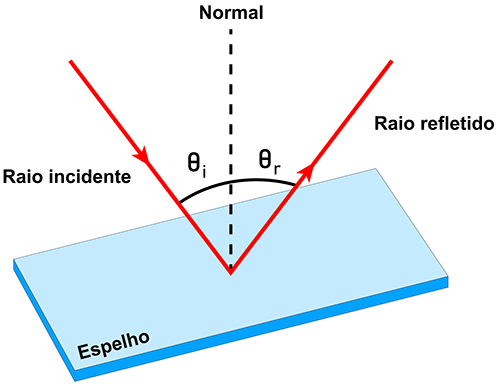
Figura 23: Reflexão da luz. Fonte: Adaptada de Dreamstime.
Com as leis da reflexão compreendidas, podemos prever o caminho da luz em espelhos e outras superfícies refletoras.
Importante
Uma superfície refletora irregular irá produzir uma reflexão difusa com raios refletidos em muitas direções aleatórias, ainda assim as leis da reflexão são obedecidas tanto na reflexão especular quanto na reflexão difusa.
Chamamos de espelho uma superfície capaz de refletir um raio de luz em uma direção bem definida, ao invés de espalhá-lo ou absorvê-lo. Se essa superfície refletora for plana, então será chamada de espelho plano. A Figura 24 nos mostra um objeto O situado a uma distância P, perpendicular, a um espelho plano. Os raios que partem do objeto O representam a luz incidente no espelho, enquanto os raios luminosos que partem do espelho representam a luz refletida. Para encontrar a distância entre o espelho e a imagem formada por ele, basta fazer o prolongamento dos raios refletidos no sentido inverso, ou seja, atrás do espelho. Assim, constataremos os prolongamentos dos raios se interceptam em um ponto que está a uma distância perpendicular i atrás do espelho.
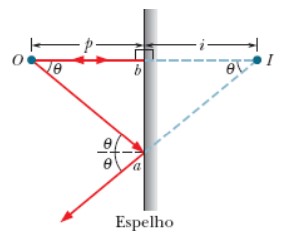
Figura 24: Espelho plano projetando a imagem i de um objeto o.
Fonte: Halliday; Resnick; Walker
(2023, p. 42).
Podemos entender o conceito de imagem como sendo uma reprodução de um objeto feita pela luz.
Fica definido que se a imagem pode se formar em uma superfície ela é uma imagem real, que existe mesmo sem a presença de um observador. Se a imagem requer o sistema visual de um observador, é uma imagem virtual.
Pense na seguinte situação: uma bola de futebol pode ser observada em um espelho plano e parece estar atrás do espelho, já que os raios luminosos que chegam aos nossos olhos vêm dessa direção, embora saibamos que, obviamente, não existe nenhuma bola atrás do espelho. Esse tipo de imagem que se forma atrás do espelho é um exemplo de imagem virtual.
Em um espelho plano, a distância entre o objeto e o espelho é igual à distância entre a imagem e o espelho. Ficou adotado, por convenção, que as distâncias dos objetos P são positivas e as distâncias i, para imagens virtuais, são negativas. Assim, podemos escrever a equação
|i| = p ou i = -p
Isso nos levará a equações com resultados corretos. A altura do objeto também é igual à altura da imagem.
Importante
As imagens reais são formadas a partir do cruzamento dos raios luminosos, enquanto as imagens virtuais são formadas pelo prolongamento desses raios. Nenhum raio luminoso passa, de fato, pela imagem virtual. Imagens virtuais não podem ser projetadas!
Quando a luz atinge uma interface suave entre dois meios materiais transparentes, como no caso da interface ar-vidro, duas situações podem ocorrer: Parte da luz será refletida na interface obedecendo as leis da reflexão e/ou parte da luz atravessa para o segundo meio de propagação. Entretanto, o raio transmitido para esse meio terá sua direção alterada quando cruzar a interface. Quando a luz é transmitida de um meio para outro e tem sua direção de propagação alterada, dizemos que houve o fenômeno de refração.
Importante
Se o raio incidente for perpendicular à interface a refração não mudará a direção de propagação da luz.
A Figura 25a nos mostra a passagem da luz por uma superfície de separação entre dois meios diferentes, ou seja, o fenômeno de refração.
“A menos que o raio incidente seja perpendicular à interface, a refração muda a direção de propagação da luz.” (Halliday; Resnick; Walker, 2023, p. 20).
Já na Figura 25b, podemos observar que a mudança na direção de propagação ocorre apenas na interface, pois dentro da água a luz se propaga em linha reta assim como no ar. Vemos ainda representados na Figura 25b o raio incidente, o raio refletido, o raio refratado, o ângulo de incidência é θ1, o ângulo de reflexão é θ′1 e o ângulo de refração é θ2, sendo estes ângulos medidos em relação à reta normal N.
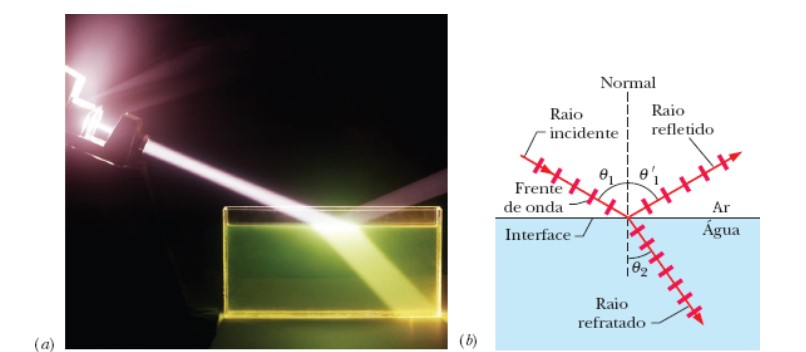
Figura 25: Fotografia e esquema mostrando a reflexão e a refração de um feixe de luz ao incidir na
interface ar-água.
Fonte: Halliday; Resnick; Walker (2023, p. 20).
Assim como a reflexão, a refração também possui sua lei. A lei da refração diz que o raio refratado está no plano de incidência e possui um ângulo de refração θ2 que se relaciona com o ângulo de incidência θ1 por meio da seguinte equação:
n1.sen θ1 = n2.sen θ2
Essa equação é conhecida como lei de Snell, e as quantidades n1 e n2 são adimensionais e chamadas de índice de refração do meio 1 e do meio 2, respectivamente. O índice de refração de um meio é dado por:

Onde v é a velocidade da luz no meio e c é a velocidade da luz no vácuo (3.108 m/s).
Quanto maior o índice de refração de um meio, menor será a velocidade na luz nele. O índice de refração do vácuo é n = 1, mas, na prática, é costume utilizar o índice de refração do ar também igual a 1. Não há meios com índice de refração inferior a 1.
Podemos comparar o ângulo de refração θ2 com o ângulo de incidência θ1. O valor relativo de θ2 depende dos valores relativos de n2 e n1, como mostra a equação abaixo:
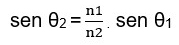
Existem três possibilidades:
- Se a luz cruzar uma interface se transmitindo de um meio 1 para um meio 2, de modo que n2 < n1, então a luz sofre um desvio se afastando da normal (Figura 26).
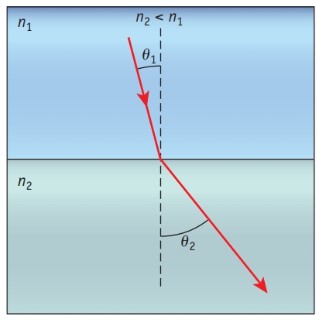
Figura 26: Luz sendo refratada entre dois meios com n2
< n1.
Fonte: Bauer; Westfall; Dias (2013, p. 24).
- Se a luz cruzar uma interface se transmitindo de um meio 1 para um meio 2, de modo que n2 > n1, então a luz sofre um desvio se aproximando da normal (Figura 27).
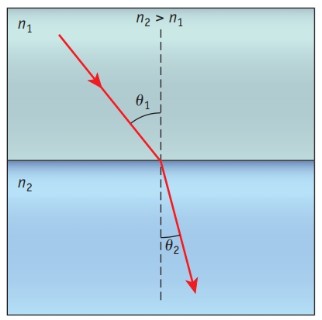
Figura 27: Luz sendo refratada entre dois meios com n2 > n1.
Fonte: Bauer;
Westfall; Dias (2013, p. 24).
- Se a luz cruzar uma interface se transmitindo de um meio 1 para um meio 2, de modo que n2 = n1, então a luz não sofre desvio (Figura 28).
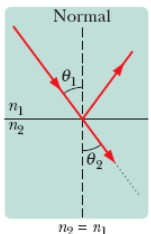
Figura 28: Luz sendo refratada entre dois meios com n2 = n1.
Fonte: Halliday;
Resnick; Walker (2023, p. 21).
Se n₂ = n₁, a luz não sofre desvio ao passar de um meio para o outro, ou seja, não há refração, e o ângulo de incidência é igual ao ângulo de refração (ou ambos são zero).
Exemplo
Um raio luminoso atravessa a interface entre água, de n1 = 1,33, e um meio misterioso, formando um angulo θ1 = 60° e θ2 = 30°, como ilustra a Figura 29. Calcule o índice de refração do meio 2.
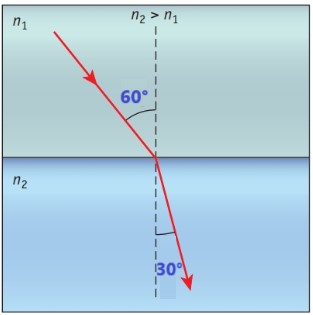
Figura 29: Raio de luz refratado. Fonte: Bauer;
Westfall; Dias (2013, p. 24).
Aplicando a lei de Snell, temos:

Curiosidade
Podemos ver, facilmente, um exemplo de refração se mergulharmos, parcialmente, um lápis em um copo transparente com água. O lápis parecerá quebrado na parte imersa em água (Figura 30), pois a luz viaja mais lentamente em água do que no ar.
Após o exemplo numérico, vamos visualizar a refração com um experimento real.

Figura 30: Experimento refração da luz. Fonte: Dreamstime.
Consideremos, agora, que a luz esteja viajando em um meio óptico de índice de refração n1 e que atravessa a interface com um meio 2, sendo n2 < n1 , a luz se afasta da normal, como já visto. Mas, à medida que aumentamos o ângulo de incidência θ1, o ângulo θ2 se aproxima da normal e, se θ1 excede o ângulo para o qual θ2=90°, não acontecerá mais refração e sim um fenômeno chamado reflexão interna total, ou seja, toda a luz é refletida internamente. O ângulo crítico θc para o qual ocorre a reflexão interna total é dado por
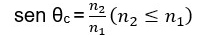
Uma aplicação moderna da reflexão interna total são as fibras ópticas, onde a onda eletromagnética sofre sucessivas reflexões internas e os dados podem ser transmitidos sem interferência e por longas distâncias.
Neste tema, estudamos os fundamentos da óptica geométrica a começar pelo modelo de raio luminoso, que é uma simplificação exagerada da propagação da luz mas que nos auxilia bastante a analisar como a luz se propaga em diferentes meios. Vimos que o modelo de raios luminosos possui três princípios básicos: a propagação retilínea da luz, a independência dos raios luminosos e a reversibilidade dos raios de luz. Observamos que todo objeto é uma fonte de raios luminosos, alguns possuem luz própria e outros apenas a refletem.
Pudemos compreender um fenômeno bastante familiar, a reflexão da luz, que acontece quando um raio luminoso atinge uma superfície e retorna ao seu meio de origem. A reflexão especular ocorre quando a luz incide em uma superfície lisa, como no caso dos espelhos e a reflexão difusa ocorre quando a luz incide em uma superfície irregular. Descremos as diferenças entre imagens virtuais, formadas atrás do espelho, e imagens reais, formadas em um local fisicamente acessível. Por fim, vimos que quando a luz atinge uma superfície de separação entre dois meios materiais transparentes, sofre um desvio em sua trajetória chamado de refração.
Além da Sala de Aula
Na leitura indicada, os autores abordam, de forma clara e detalhada, o fenômeno da refração, mostrando como a luz viaja a velocidades diferentes em materiais opticamente transparentes e como isso se relaciona ao conceito de profundidade aparente. Adiante, abordam a questão do ângulo crítico de incidência e como ao atingir o ângulo limite ocorre a reflexão interna total da luz. Diversas aplicações desses fenômenos são explicadas, como por exemplo, fibra óptica, miragens, dispersão cromática e polarização por reflexo.
Todos esses pontos são tratados por Bauer, Westfall e Dias (2013); por isso, faça a leitura da página 24 a 33 do livro Física para universitários, disponível na Minha Biblioteca.
Lembre-se de que, para iniciar a leitura do livro sinalizado, é necessário fazer login na Minha Biblioteca.
Título do livro/artigo: Física para universitários
Páginas indicadas: 24 a 33
Referência: BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para
universitários. Porto Alegre: Bookman, 2013.
Na leitura indicada, o autor aborda a física das ondas, inicialmente, fazendo um contraste com o modelo macroscópico, até chegar ao modelo de onda. O autor desenvolve uma análise das ondas que se propagam a partir de uma fonte através de algum meio, como as ondulações que se propagam na água e analisa as ondas que são capazes de propagar no vácuo, as ondas eletromagnéticas. A equação fundamental de onda, que relaciona o comprimento de onda e o período, é explicada por meio de cinco gráficos instantâneos de onda senoidal que evidenciam essa relação.
Todos esses pontos são tratados por Randall D. Knight (2009); por isso, faça a leitura da página 182 a 194 do livro Física uma abordagem estratégica: termodinâmica óptica, disponível na Minha Biblioteca.
Lembre-se de que, para iniciar a leitura do livro sinalizado, é necessário fazer login na Minha Biblioteca.
Título do livro/artigo: Física uma abordagem estratégica: termodinâmica
óptica
Páginas indicadas: 182 a 194
Referência: KNIGHT, R. D. Física uma abordagem estratégica:
termodinâmica óptica. 2. ed. Porto Alegre: Bookman, 2009. v. 2.
Neste estudo de caso, analisaremos como ondas sonoras de alta frequência são utilizadas em exames médicos e podem, até mesmo, salvar vidas. As ondas sonoras de alta frequência são os chamados ultrassons, que possuem frequências muito acima do espectro audível e encontram-se em faixa superior a 20 000 Hz. Qualquer tipo de onda pode sofrer reflexão, no caso dos ultrassons chamaremos a reflexão de eco, que acontece ou não, no caso dos exames médicos, a depender da presença de lesões no tecido humano.
Considere a seguinte situação: um ciclista que pedalava calmamente, a cerca 3 m/s, ao tentar desviar de um buraco, caiu e bateu a cabeça em um obstáculo. Ao chegar ao hospital, mesmo que aparentasse não estar gravemente ferido, foi submetido a um exame de ultrasson cranial. O aprelho de ultrassonografia possui um dispositivo chamado de transdutor, que faz a emissão das ondas sonoras para dentro do corpo no e o mesmo dispositivo capta o eco dessas ondas, que são refletidas ao encontrar algum elemento no corpo. A partir do eco, é possível medir densidade, composição, tamanh humaos e distâncias.
A existência de uma lesão cerebral no ciclista poderá ser verificada por meio da detecção do sinal de ultrassom que a própria lesão reflete. A figura a seguir ilustra que a região de tecido encefálico a ser investigada no exame é limitada por ossos do crânio. Sobre um ponto do crânio se apóia o emissor/receptor de ultrassom.
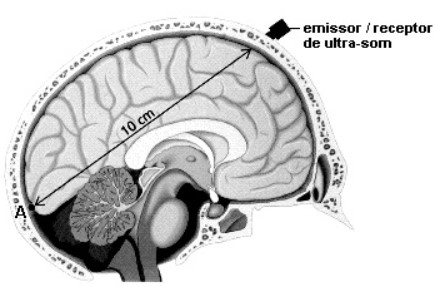
Fonte: DOCA, R. H.; BISCUOLA, G. J.; BÔAS, N. V. Tópicos de física 1
- Mecânica. 21. ed. São Paulo:
Saraiva, 2012. p. 55.
Questionamentos para reflexão:
- Suponha a não existência de qualquer tipo de lesão no interior da massa encefálica. Qual seria o tempo gasto para registrar o eco proveniente do ponto 𝐴 da figura? Dado: velocidade do ultrassom no cérebro =1540 m/s.
- Sabendo que há uma lesão, de fato, pois o tempo gasto para registrar o eco foi de 0,5.10-4s, qual é a distância do ponto lesionado até o emissor?
- Qual é a distância do ponto lesionado até o ponto A?
- O ciclista conseguiu ouvir os ultrassons?
Assista às videoaulas a seguir, que têm como objetivo reforçar os conteúdos abordados nesta unidade de maneira didática para embasar os conceitos e teorias trabalhados. Esperamos que contribuam significativamente para seu aprendizado e que a busca pelo conhecimento não se encerre neste percurso de aprendizagem.
Neste infográfico, trataremos do movimento ondular, o movimento no qual a transferência de energia ocorre sem que haja transporte de matéria. Definiremos o conceito de onda e veremos como ondas podem ser classificadas quanto à sua natureza e quanto a sua direção de propagação. Veremos exemplos de ondas transversais, longitudinais, mecânicas e eletromagnéticas.

Nesta unidade, focamos em um tipo de movimento muito revelante para o estudo das ondas, o movimento periódico, aquele no qual após decorrido um intervalo de tempo fixo, o corpo retorna a sua posição inicial. Partindo disso, pudemos analisar o movimento oscilatório, um movimento periódico marcado pela presença de uma inversão no sentido do movimento em intervalos de tempo regulares. Analisamos o movimento harmônico simples para a compreensão de diversos fenômenos físicos.
Estudamos o movimento ondulatório, definimos o conceito de onda e vimos diversos exemplos conhecidos de propagação de ondas, a luz, o som, as ondas na água e um pulso em uma corda. As ondas podem ser classificadas de acordo com sua origem, mecânicas ou eletromagnéticas e de acordo com sua direção de propagação, longitudinal ou transversal. Identificamos os elementos que compõem uma onda, período, frequência, comprimento de onda, amplitude e frequência angular.
Enfim, definimos o modelo de raios luminosos, um recurso para análise de sistemas ópticos e estabelecemos os princípios de propagação, independência e reversibilidade de raios luminosos, o que fundamenta o estudo da óptica geométrica. Analisamos o fenômeno de reflexão da luz, seus tipos e as leis que a regem e, de igual forma, conceituamos a refração da luz, a lei da refração e a lei de Snell. Finalizamos com o estudo do fenômeno da reflexão total e as condições para sua ocorrência.
Para sua autorreflexão:
- Identificou as condições necessárias para classificar um movimento como MHS?
- Denominou os elementos que compõem uma onda e definiu-os?
- Distinguiu as diferenças entre imagens reais e virtuais?
BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: Bookman, 2013.
HALLIDAY, D.; RESNICK, R.; KRANE, K. S. Física. 5. ed. Rio de Janeiro: LTC, 2017. v. 2.
HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de Física - Óptica e Física Moderna. 12. ed. Rio de Janeiro: LTC, 2023. v. 4.
JEWETT JR., J. W.; SERWAY, R. A. Física para cientistas e engenheiros - Oscilações; ondas e termodinâmica. 2. ed. São Paulo: Cengage Learning Brasil, 2013. v. 2.
KNIGHT, R. D. Física uma abordagem estratégica: termodinâmica óptica. 2. ed. Porto Alegre: Bookman, 2009. v. 2.
MARQUES, G. da C. Movimento Harmônico Simples (MHS). USP, 2024. Disponível em: https://midia.atp.usp.br/plc/plc0002/impressos/plc0002_11.pdf. Acesso em: 8 out. 2024.
MARQUES, G. da C.; UETA, N. Óptica - Reflexão. IF.USP, 2024. Disponível: https://efisica2.if.usp.br/pluginfile.php/5830/mod_resource/content/0/reflexao_refra%C3%A7%C3%A3o_reflex%C3%A3o_leis.pdf. Acesso em: 8 out. 2024.
TIPLER, P. A.; MOSCA, G. Física para cientistas e engenheiros - Mecânica, oscilações e ondas, termodinâmica. 6. ed. Rio de Janeiro: LTC, 2009. v. 1.







