Nesta unidade, definiremos o conceito de equilíbrio termodinâmico e analisaremos como ele se relaciona com as propriedades macroscópicas de um sistema. Veremos também outros conceitos fundamentais para o estudo da termodinâmica, o conceito de estado da matéria, propriedades intensivas e extensivas, processos e ciclos termodinâmicos. Conheceremos a lei zero da termodinâmica que define o conceito de temperatura e explica o equilíbrio térmico.
A seguir, analisaremos como a energia pode ser transferida entre um sistema e seu ambiente, tanto na forma de calor quanto como trabalho. Definiremos uma equação para calcular o trabalho realizado por um sistema em um processo que ocorre a pressão constante. Por fim, conheceremos a primeira lei da termodinâmica, que mostra que calor e trabalho podem ser transformados em energia térmica, sem que nenhuma energia se perca.
Veremos o que são processos reversíveis e irreversíveis e como se classificam os processos da natureza, na sua maioria. Discutiremos a segunda lei da termodinâmica e veremos sua importância para a ciência. Analisaremos dispositivos capazes de converter energia térmica em energia mecânica, as máquinas térmicas. Por fim, abordaremos o ciclo de Carnot, sob o qual opera uma máquina térmica idealizada chamada de máquina de Carnot.
Em sua leitura, foque na definição de fase, estado da matéria e propriedades da matéria, assim como suas duas classificações. Observe e guarde o conceito de equilíbrio termodinâmico e a importância do conceito de quase equilíbrio para o estudo dos processos. Dê atenção ao conceito de ciclo termodinâmico e ao fato de que, ao final de um ciclo, todas as propriedades do sistema retornam ao valor inicial. Atente-se ao enunciado da lei zero da termodinâmica, especialmente à sua definição de equilíbrio térmico. Ao adentrarmos nos temas seguintes, atente-se à definição de trabalho e à equação que permite calculá-lo em processos adiabáticos. Note que, em processos isocóricos, o trabalho é nulo.
Dê atenção especial à definição da primeira lei da termodinâmica, mas tenha em mente que trabalho e calor não são variáveis de estado. A primeira lei pode ser aplicada a diferentes processos; foque nas restrições e na forma da primeira lei para esses processos. Por fim, observe o que são máquinas térmicas, como funcionam e como calcular seu rendimento. E fique atento aos refrigeradores, que, diferentemente das máquinas térmicas, retiram calor do reservatório frio e o rejeitam para o reservatório quente. Note também as três formas de enunciar a segunda lei da termodinâmica e a restrição que se aplica às máquinas térmicas.
Nos temas a seguir, você irá aprofundar seu conhecimento com o estudo dos assuntos específicos desta unidade e, ao final, deverá atingir os seguintes objetivos de aprendizagem:
- Relacionar os conceitos de equilíbrio térmico com a Lei Zero da Termodinâmica;
- Reconhecer a relação entre trabalho e calor em sistemas macroscópicos;
- Utilizar a equação do trabalho para processos isobáricos;
- Identificar a primeira e segunda lei da termodinâmica; e
- Reconhecer a importância do cálculo do rendimento de diferentes máquinas térmicas.
Tema 1 - Temperatura e Equilíbrio Termodinâmico
Neste tema, veremos alguns conceitos que fundamentam a física termodinâmica e que nos permitirão aprofundar nesta área mais adiante. Mencionaremos que uma substância pode existir em diferentes fases e definiremos o que é o estado de uma substância. Como as propriedades macroscópicas de uma substância descrevem o estado da matéria, analisaremos o significado de propriedade e daremos uma definição conceitual. Seguindo na análise das propriedades macroscópicas, apresentaremos duas classes gerais nas quais elas podem ser enquadradas: intensivas e extensivas.
Apontaremos como as propriedades de um sistema se relacionam com o equilíbrio termodinâmico e abordaremos um conceito básico da termodinâmica, a temperatura. Elucidaremos também um postulado denominado lei zero da termodinâmica, que serve de base para a compreensão do que é temperatura e que introduz o conceito de equilíbrio térmico. Por fim, veremos como esta lei permitiu a construção e utilização de termômetros.
Equilíbrio Termodinâmico, Processos e Ciclos
Vamos considerar uma certa massa de água. Precisamos admitir que essa quantidade de água pode existir de diversas formas diferentes. Inicialmente, ela poderia ser líquida e, depois de ser aquecida, tornar-se vapor ou, ainda, pode ser sólida se for resfriada. Chamaremos de fase uma quantidade de matéria totalmente homogênea, e, caso coexistam mais de uma fase, elas estarão separadas entre si pelo que chamamos de fronteiras das fases. Para cada fase, a substância pode existir a várias pressões e temperaturas; então, em termodinâmica, dizemos que essa substância existe em vários estados.
Podemos identificar o estado de uma substância através de propriedades macroscópicas observáveis, como aquelas com as quais já estamos familiarizados: temperatura, pressão e massa específica. Compreenda que cada uma das propriedades de uma substância, em um dado estado, terá apenas um mesmo valor determinado. Logo, cada uma dessas propriedades terá sempre o mesmo valor em um dado estado, e isso não depende do modo pelo qual a substância atingiu esse estado.
Em outras palavras, uma propriedade é uma quantidade que depende do estado, mas não depende do caminho através do qual o sistema chegou ao determinado estado. De forma análoga, o estado também será descrito por meio das propriedades. Podemos classificar as propriedades termodinâmicas como intensivas ou extensivas. Uma propriedade será considerada intensiva quando for independente da massa, enquanto uma propriedade extensiva terá um valor que varia diretamente com a massa.
Se uma quantidade de certa substância se encontra em determinado estado, ao ser dividida em duas partes iguais, ambas as partes apresentarão o mesmo valor para propriedades intensivas e metade do valor das propriedades extensivas em relação à massa original. A temperatura, a pressão e a massa específica são propriedades intensivas; já o volume é uma propriedade extensiva.
Comumente fazemos menção às propriedades de um sistema, ou seja, o valor da propriedade tem significância para todo o sistema e não apenas isso, também implica o que chamamos de equilíbrio. Existem diversos tipos de equilíbrio. Vamos supor que o gás mostrado na figura abaixo seja um sistema e que todo o gás possua a mesma temperatura; então o sistema está em equilíbrio térmico. Note que a temperatura é uma propriedade do sistema.
O equilíbrio mecânico é aquele que se relaciona com a pressão; ou seja, se um sistema estiver em equilíbrio mecânico e isolado do meio exterior, não haverá a tendência de a pressão variar ao longo do tempo. Sabemos que existe uma variação de pressão no gás que ocorre em função da altura, devido à atuação do campo gravitacional; mas ainda assim, sob as condições de equilíbrio, a pressão não tende a se alterar em qualquer ponto.
Em geral, nos problemas termodinâmicos, essa variação de pressão com a altura é tão ínfima que costuma ser desprezada. Temos ainda o equilíbrio químico, que ocorre quando a velocidade de transformação de reagentes em produtos é exatamente a mesma que a velocidade de transformação de produtos em reagentes. Enfim, dizemos que um sistema está em equilíbrio termodinâmico se houver equilíbrio em relação a toda mudança de estado possível.
Se houver alteração em pelo menos uma propriedade do sistema, então houve uma mudança de estado, e a sucessão de mudanças de estado é chamada de processo. Pensemos agora no equilíbrio de um sistema quando ocorre uma mudança de estado. A figura a seguir ilustra um sistema que consiste em um gás confinado em um recipiente com êmbolo móvel e sobre o qual estão alguns “pesos”.
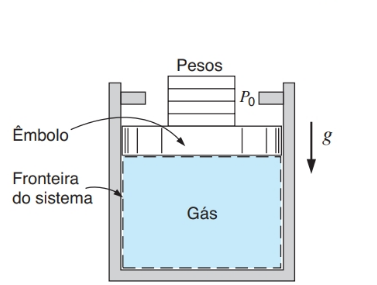
Figura 1: Exemplo de processo de quase equilíbrio. Fonte: Borgnakke (2018, p. 27).
Ao retirar um dos pesos, o êmbolo se deslocará para cima, a pressão diminuirá enquanto o volume específico aumenta. O que aconteceu no instante em que o peso foi removido foi que o equilíbrio mecânico deixou de existir, mas o êmbolo subiu até que o equilíbrio mecânico foi restabelecido. A grande questão é que, se as propriedades só podem descrever o estado de um sistema quando ele está em equilíbrio termodinâmico, seria possível descrever o estado de um sistema durante um processo?
Um processo real só acontece quando não há equilíbrio; portanto, para descrever os estados de um sistema ao longo de um processo, utilizaremos a definição de processo ideal, também chamado de processo de quase equilíbrio. Em um processo de quase equilíbrio, o desvio do equilíbrio termodinâmico é infinitamente pequeno; assim, todos os estados pelos quais o sistema passar poderão ser classificados como estados de equilíbrio.
Esse recurso permite modelar, de forma precisa, muitos dos processos reais como processos de quase equilíbrio. Retornando ao exemplo da figura, podemos admitir que se os “pesos” forem bem pequenos e retirados um a um, teremos um processo que pode ser definido como um processo de quase equilíbrio. Se, na situação da figura, os “pesos” forem removidos de uma só vez, o êmbolo subirá abruptamente, atingindo os limitadores.
Neste caso, teríamos um processo de não equilíbrio e, em nenhum instante, durante a mudança de estado, o sistema atingiria o equilíbrio. Quando tratamos de processos de não equilíbrio, precisaremos nos limitar a uma descrição do sistema antes da ocorrência do processo e depois de sua ocorrência, quando o equilíbrio já foi restabelecido. Existem muitos processos que podem ser caracterizados por alguma propriedade que se mantém constante e, para isso, usaremos o prefixo “iso”.
Por exemplo, se durante um processo a temperatura se manteve constante, dizemos que o processo é isotérmico; se a pressão foi a propriedade que se manteve constante, o processo será chamado isobárico, e se o volume se mantiver constante, o processo será chamado de isocórico, isovolumétrico ou, ainda, isométrico. Comumente, em termodinâmica, fala-se que determinado sistema realizou um ciclo, o que quer dizer que o sistema, que se encontrava em um dado estado inicial, passou por algumas mudanças de estado, ou processos, mas retornou ao seu estado inicial.
Importante
Ao final de um ciclo termodinâmico, todas as propriedades do sistema apresentam os mesmos valores iniciais.
Temperatura e Lei Zero da Termodinâmica
A noção comum de temperatura, que é subjetiva, não é de modo algum confiável. Podemos constatar isso a partir de uma situação cotidiana comum. Se, em um dia frio, você colocar a mão em uma maçaneta de porta feita de material metálico e, em seguida, tocar na porta de madeira, terá a sensação de que a maçaneta tem uma temperatura muito menor que a porta de madeira, embora ambas estejam à mesma temperatura.
Ao colocar a mão em um objeto, você não está medindo sua temperatura e sim a capacidade do material de transferir calor, sua condutividade térmica. Como o metal é um melhor condutor de calor, irá absorver uma maior quantidade de calor da sua mão do que a madeira, e você terá a sensação de que ele está mais frio. Nesse caso, a mão fornece uma medida incorreta de temperatura. Sendo assim, precisaremos de uma maneira correta e confiável de medir temperatura.
Tomemos como exemplo dois sistemas A e B, ilustrados na figura a seguir, que podem ser dois blocos metálicos. Se esses sistemas estiverem isolados, tanto um do outro quanto de sua vizinhança, de tal forma que nem matéria nem energia possam ser transferidas para o sistema, pois o sistema é cercado por paredes impermeáveis e adiabáticas (não permite troca de calor), as variações nas propriedades medidas de um dos sistemas não poderão influenciar as propriedades do outro sistema.
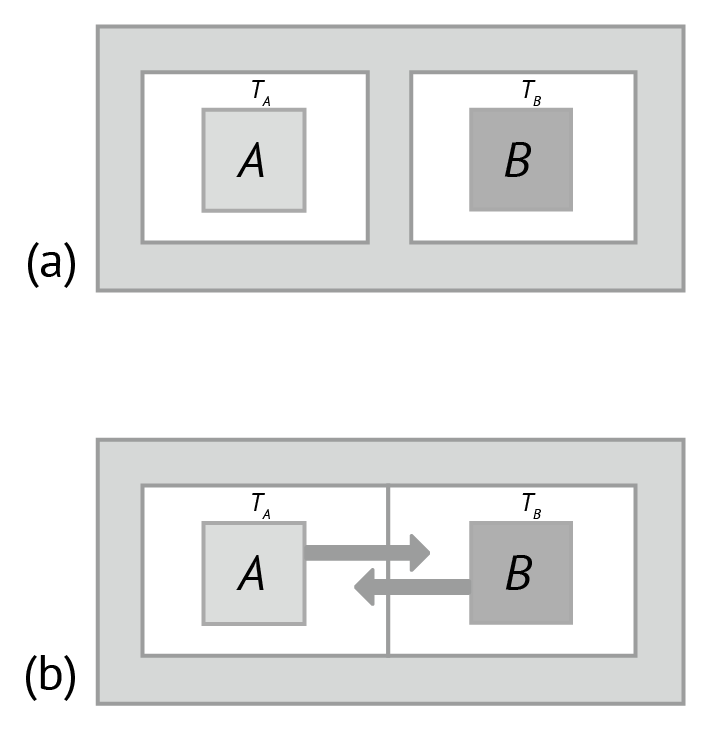
Figura 2: (a) Sistemas A e B separados por paredes adiabáticas; (b) sistemas A e B separados por paredes diatérmicas. Fonte: Halliday (2017, p. 206).
Se a parede adiabática que separa os sistemas A e B for substituída por uma parede diatérmica, que é uma parede condutora de calor, podemos dizer que os sistemas estão em contato térmico. Caso haja transferência de calor entre os sistemas, suas propriedades irão variar, inicialmente de forma rápida, mas isso ocorrerá mais lentamente ao longo do tempo, até que todas as propriedades de cada sistema se aproximem de valores constantes, o que significa que os sistemas estão em equilíbrio térmico um com o outro.
Sendo assim, temos agora uma forma de verificar se dois corpos ou sistemas estão em equilíbrio térmico entre si, colocando-os em contato térmico; caso suas propriedades se mantenham constantes, eles estarão em equilíbrio térmico, mas, se as propriedades variarem, não estarão. O problema é que nem sempre é conveniente, ou até mesmo possível, colocar os sistemas em contato através de uma parede diatérmica, então o conceito de equilíbrio térmico foi generalizado, de modo que esse contato não seja necessário.
Desta forma, para testar se dois sistemas A e B estão em equilíbrio térmico um com o outro, será necessário utilizar um terceiro sistema C. Ao colocarmos C em contato com A e depois em contato com B, podemos determinar se A e B estão em equilíbrio térmico, mesmo sem estabelecer contato entre A e B. O postulado que resume essa situação é chamado de lei zero da termodinâmica, que costuma ser expresso como: Se dois sistemas A e B estão cada um em equilíbrio térmico com um terceiro sistema C, então A e B estão em equilíbrio térmico entre si.
Curiosidade
A lei zero surgiu no século XX, na década de 1930, muito depois da primeira e segunda leis da termodinâmica terem sido propostas e aceitas. A lei zero serve de base ao conceito de temperatura, o qual é fundamental para as primeiras e segundas leis. Uma vez que a lei que estabelece o conceito de temperatura deve ter um número menor, ela é chamada de lei zero (Halliday, 2017, p. 207).
Se dois sistemas estão em equilíbrio térmico, então os dois possuem a mesma temperatura. Vamos supor que dois gases tenham, inicialmente, valores diferentes de pressão, temperatura e volume. Ao colocá-los em contato e aguardar certo tempo, de modo que atinjam o equilíbrio térmico, suas pressões e volumes ainda terão valores diferentes; suas temperaturas, entretanto, sempre serão iguais no equilíbrio térmico. “É somente através deste argumento, baseado no equilíbrio térmico, que a noção de temperatura pode ser introduzida na física” (Halliday, 2017, p. 207).
Um termômetro funciona como o sistema C a que se refere a lei zero da termodinâmica. Se o termômetro é posto, separadamente, em contato com o sistema A e atinge o equilíbrio térmico, depois colocado, separadamente, em contato com o sistema B e atinge o equilíbrio térmico, se apresentar a mesma leitura para ambos, isso significa que A e B estão na mesma temperatura.
Observe que, para verificar se dois sistemas estão na mesma temperatura, não é necessário utilizar uma escala termométrica. Por exemplo, se o referido termômetro (sistema C) for de mercúrio, não é necessário que ele tenha marcações em graus; basta medir a altura da coluna de mercúrio em contato com o corpo A e depois medir a altura da coluna de mercúrio quando estiver em contato com o corpo B. Se essas alturas forem iguais, então A e B estão na mesma temperatura.
A declaração da lei zero da termodinâmica acerca da temperatura é expressa da seguinte forma: “Existe uma grandeza escalar chamada de temperatura, que é uma propriedade de todos os sistemas termodinâmicos em equilíbrio. Dois sistemas estão em equilíbrio térmico se e somente se as suas temperaturas são iguais” (Halliday, 2017, p. 207). Concluímos que a lei zero definiu o conceito de temperatura e permitiu, inclusive, que os termômetros fossem construídos e utilizados.
Neste tema, vimos alguns conceitos fundamentais para dar início ao estudo da termodinâmica. Abordamos que a fase de uma substância pode ser definida como uma quantidade de matéria totalmente homogênea e que, em cada fase, uma substância pode existir a várias pressões e temperaturas, o que chamamos de diferentes estados. A descrição do estado da matéria, por sua vez, pode ser identificada ou descrita pelas propriedades macroscópicas, como temperatura e pressão, por exemplo. Observamos que uma propriedade pode ser definida como uma quantidade que irá depender do estado do sistema, mas sem depender dos meios pelos quais o sistema chegou ao estado considerado.
Analisamos que as propriedades termodinâmicas podem ser classificadas como intensivas, se forem independentes da massa, ou como extensivas, se variarem de modo proporcional à variação de massa. Concluímos que, para que um sistema esteja em equilíbrio termodinâmico, é necessário que esse sistema se encontre simultaneamente em equilíbrio térmico, equilíbrio mecânico e equilíbrio químico. Por fim, trouxemos a lei zero da termodinâmica, que define temperatura e equilíbrio térmico, servindo de base para as outras leis da termodinâmica que veremos a seguir.
Tema 2 - Primeira Lei da Termodinâmica e Transformações Termodinâmicas
A termodinâmica surgiu paralelamente à Revolução Industrial devido a um estudo sistemático que tinha como alvo a utilização da energia térmica para produzir movimento e trabalho mecânico, o que deu origem ao seu nome: termo + dinâmica (termodinâmica). O foco da termodinâmica aplicada à engenharia ainda é o estudo dos motores e geradores de energia, mas, enquanto ciência, a termodinâmica abrange todas as formas de energia, incluindo as relacionadas aos organismos vivos.
O objetivo central do estudo da termodinâmica consiste em compreender as transformações de energia e quão eficientes elas podem ser. A própria termodinâmica dita os limites acerca do rendimento dessas transformações energéticas e, à medida que avançamos no entendimento desses limites, podemos entender e suprir as necessidades reais da sociedade moderna no que diz respeito aos dispositivos capazes de transformar energia em trabalho útil.
Calor e Trabalho
Sabemos que o motor a vapor foi o que moveu a Revolução Industrial, já que, para ferver água e gerar vapor a alta pressão, utilizava-se a queima de carvão ou madeira. Quando o vapor se expandia, ele empurrava um pistão que, atrelado a engrenagens, fazia a roda das pás girar, colocando o maquinário em funcionamento e até mesmo impulsionando locomotivas muito pesadas. Embora os seres humanos já utilizassem calor há vários anos, tanto na culinária quanto na metalurgia, com o motor a vapor era diferente; pela primeira vez, a humanidade estava utilizando calor para realizar trabalho mecânico.
Ao observarmos um recipiente contendo água quente, não podemos determinar se a energia térmica foi transferida para essa água ou se foi realizado trabalho sobre a água, pois tanto o calor quanto o trabalho são transferências de energia entre um sistema e sua vizinhança. Devemos lembrar que o calor é uma forma de energia que flui de um sistema para outro quando há diferença de temperatura entre eles e que o calor sempre flui do sistema de maior temperatura para o sistema de menor temperatura até que alcancem o equilíbrio térmico.
Quanto ao trabalho, podemos dizer que é uma energia transferida entre um sistema e sua vizinhança quando houver uma força resultante atuando sobre o sistema ao longo de uma determinada distância. De forma simplificada, a vizinhança, ou uma força exercida pela vizinhança, realiza trabalho sobre o sistema. Se não houver força resultante atuando sobre o sistema, ele estará em equilíbrio mecânico. Para analisar como a energia pode ser transferida entre um sistema e seu entorno, como calor ou trabalho, vamos considerar um sistema formado por um cilindro cheio de um gás ideal, com um pistão livre para se mover.
O gás contido no cilindro possui uma temperatura T, uma pressão P e um volume V, e partiremos do pressuposto de que as paredes laterais do cilindro são adiabáticas, ou seja, não permitem que o calor adentre. O gás encontra-se em contato térmico com um reservatório infinito, que nada mais é do que um reservatório tão grande que sua temperatura T não varia, ainda que haja um fluxo de energia para dentro ou para fora dele.
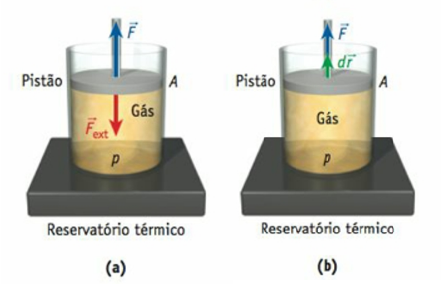
Figura 3: Cilindro com um pistão contendo gás ideal (a) uma força externa empurra o pistão; (b) a força externa é retirada. Fonte: Bauer (2012, p. 194).
Observe que na figura a uma força externa $\vec{F}$ está empurrando o pistão para baixo e o gás, por sua vez, empurra o pistão de volta com uma força $\vec{F}$, que é dada pela pressão P do gás multiplicada pela área A do pistão (F = P.A). Vamos considerar que esse gás tenha um estado inicial descrito por uma pressão inicial Pi, um volume inicial Vi e uma temperatura inicial Ti, e um estado final descrito por uma pressão final Pf, um volume final Vf e uma temperatura final Tf.
Estamos supondo que as mudanças sofridas pelo gás ocorrem de forma tão lenta que ele permanece próximo do equilíbrio, e, assim, é possível realizar as medições de pressão, volume e temperatura. Essa progressão que vai do estado inicial até o final é um processo termodinâmico, e, durante esse processo, a energia térmica pode fluir para o gás (calor positivo) ou para fora dele (calor negativo).
Note que, na figura b, a força externa é retirada e, com isso, o pistão é movido uma distância dr. Sendo assim, o trabalho realizado pelo gás nesse processo termodinâmico é dado por:
$d w=\vec{F} d \vec{r}=P(A d r)=P d V$
Sabendo que A dr corresponde à mudança de volume do sistema, o trabalho que o sistema realiza ao passar do estado inicial para o final é dado por:
$W=\int d w=\int_{V_i}^{V_f} P d V$
Enquanto o volume muda, a pressão também pode variar, mas, caso ela seja constante, o trabalho realizado pelo sistema será dado por:
$W=P\left(V_f-V i\right)$ ⇨ Pressão Constante
Exemplo
Tem-se um sistema formado por um conjunto cilindro-êmbolo onde vários pesos pequenos são colocados sobre o êmbolo. Sabe-se que a pressão inicial é 100 KPa e o volume inicial do gás é 0,05 m³. Ao posicionar um bico de Bunsen embaixo do cilindro o gás se expandiu e seu volume aumentou para 0,1m³, enquanto a pressão manteve-se constante. Calcule o trabalho realizado pelo sistema durante esse processo.
Aplicando a equação do trabalho para pressão constante, temos:
W = P (Vf – Vi)
W = 100 . (0,1 – 0,05)
W = 5 KJ
Importante
O sinal algébrico do trabalho não é, simplesmente, uma convenção arbitrária, tampouco tem a ver com a escolha do sistema de coordenadas. Em vez disso, ele nos informa sobre o sentido em que se dá a transferência de energia” (Knight, 2009, p. 90).
A figura abaixo apresenta gráficos de pressão x volume, conhecidos como diagramas PV, e cada parte da figura mostra caminhos distintos pelos quais a pressão e o volume de um sistema se alteram de uma condição inicial i para uma condição final f.

Figura 4: Três processos diferentes em diagramas PV. Fonte: Bauer (2012, p. 175).
Na parte (a) da figura, vemos um processo que vai de um ponto inicial i até um ponto final f, onde a pressão diminui à medida que o volume cresce. Como há um aumento de volume, o trabalho realizado pelo gás é positivo. Já na parte (b) da figura, o processo vai de um ponto inicial a um ponto final através de um ponto intermediário m; inicialmente, a pressão se mantém constante enquanto o volume aumenta, após isso, a pressão diminui enquanto o volume permanece constante. Como há aumento de volume, o trabalho realizado pelo gás é positivo, mas só há trabalho na primeira parte do processo, já que na segunda parte o volume é constante.
Na parte (c) da figura, podemos ver novamente um processo que se inicia em um ponto inicial i e que termina em um ponto final f, a partir de um ponto intermediário m. Nesse caso, inicialmente a pressão diminui e o volume se mantém constante, mas, a seguir, a pressão passa a ser constante enquanto o volume aumenta; ou seja, o trabalho realizado pelo gás é positivo, mas se origina apenas no segundo passo, já que no primeiro o volume não se altera. Em ambos os processos, o trabalho realizado pelo sistema (com sinal positivo, já que o volume aumenta) pode ser dado pela área sob a curva mostrada pelo sombreado verde.
Esse tipo de processo depende do caminho, já que o trabalho realizado e a energia térmica transferida para o sistema irão depender de como o sistema se move do ponto inicial até o final. A figura a seguir, por exemplo, mostra a reversão dos processos mostrados na figura acima, começando nos pontos finais da mesma e permanecendo ao longo do mesmo caminho até os pontos iniciais. Note que, em cada um desses casos, a área sob a curva ainda representa o trabalho realizado pelo gás, mas agora com sinal negativo, já que o volume do gás diminui.

Figura 5: Caminhos de três processos em diagrama PV. Fonte: Bauer (2012, p. 175).
Se o processo que leva o sistema de um estado inicial até um estado final, em um diagrama PV, ocorrer de modo que percorra um caminho que o faça retornar ao seu ponto de origem, teremos um caminho fechado, ou seja, um ciclo termodinâmico. Nos ciclos termodinâmicos, se o caminho girar no sentido horário, isso representa um trabalho positivo; se girar no sentido anti-horário, representa um trabalho negativo.

Figura 6: Dois processos de caminho fechado em diagramas PV. Fonte: Bauer (2012, p. 176).
Na figura a vemos que no caminho de i para m1 o trabalho é positivo, pois o volume aumenta e de m2 para m3 o trabalho é negativo, já que o volume diminui. Essa adição do trabalho positivo e negativo gera um trabalho líquido positivo realizado pelo sistema, dado pela área do retângulo verde. Nesse caso, o calor é positivo.
Na figura b, onde o processo acontece no sentido inverso, o caminho de m1 para m2 corresponde a um trabalho positivo, pois o volume aumenta, mas de m3 para o ponto final f o trabalho é negativo, pois o volume diminui. Nesse caso, o trabalho líquido realizado pelo sistema é negativo, sua magnitude é fornecida pela área do retângulo laranja, e o calor é negativo.
O trabalho em processos com gases ideais pode ocorrer das seguintes formas:
- Processo Isocórico: É um processo que ocorre a volume constante e por consequência, o trabalho nesse processo é zero.
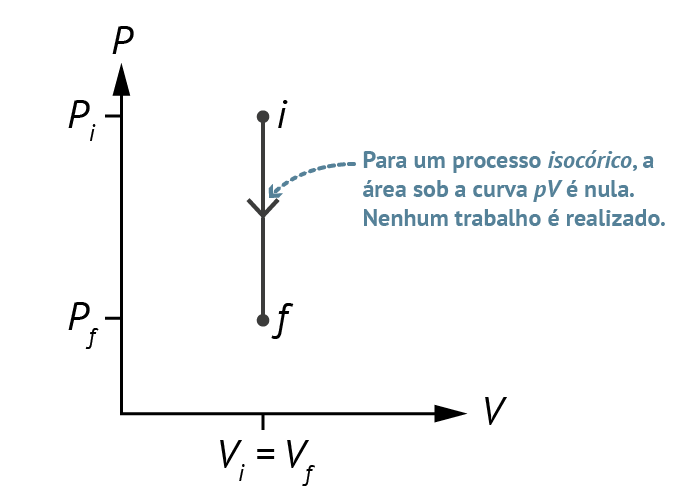
Figura 7: Gráfico PV de um processo isocórico. Fonte: Knight (2009, p. 511).
- Processo Isobárico: É um processo em que o volume inicial Vi do sistema se altera até chegar a um volume final Vf, figura abaixo, e, embora o volume varie, a pressão se mantém constante e o cálculo do trabalho é feito pela equação W = p.∆V.
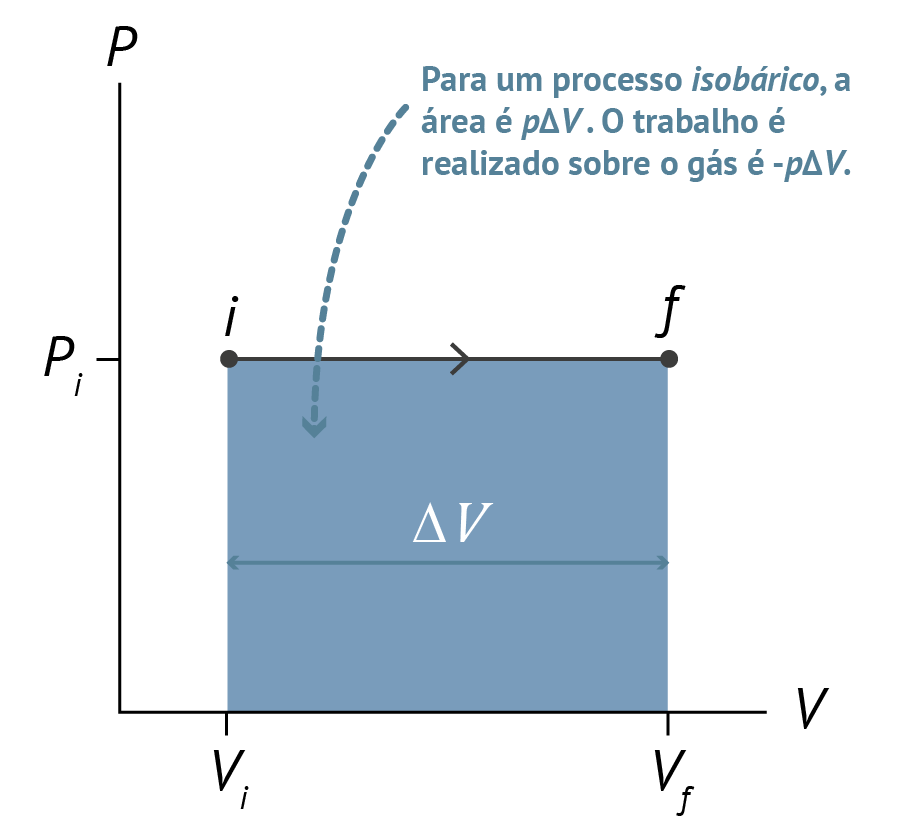
Figura 8: Gráfico PV de um processo isobárico. Fonte: Knight (2009, p. 511).
- Processo Isotérmico: Nesse processo representado na figura abaixo, a pressão e o volume variam e apenas a temperatura se mantém constante. Sabemos, por meio da equação dos gases ideais, como a pressão se comporta em função do volume, p = nRT/V, logo, o trabalho em um processo isotérmico é dado por:
$\mathrm{W}=\mathrm{nRT} \ln \left(\frac{V_i}{V_f}\right)$
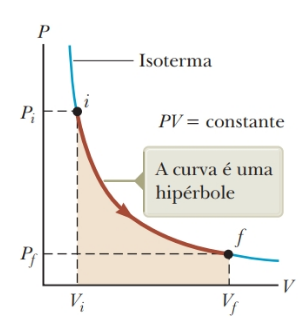
Figura 9: Diagrama PV de uma expansão isotérmica. Fonte: Jewett Jr. (2013, p. 147).
A unidade de medida do trabalho é a mesma utilizada para outras formas de energia: o Joule (J).
O físico James Prescott Joule realizou um experimento clássico em 1843, onde demonstrou que a energia mecânica de um objeto poderia ser convertida em energia térmica. Joule fez isso por meio de um dispositivo que consistia em uma grande massa sustentada por uma corda, que passava por uma polia e era amarrada em torno de um eixo, como mostra a figura abaixo.
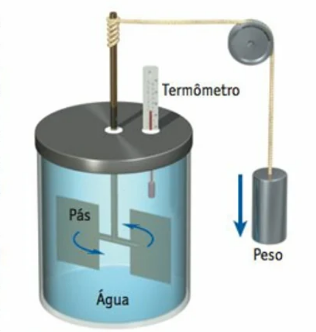
Figura 10: Dispositivo utilizado por Joule no experimento que demonstrou que a energia mecânica podia ser transformada em energia térmica. Fonte: Bauer (2012, p. 173).
À medida que a massa descia, a corda era desenrolada e movia um par de pás em um recipiente com água. Com isso, Joule conseguiu demonstrar que o aumento da temperatura da água estava diretamente relacionado ao trabalho mecânico realizado pelo objeto em queda. Foi dessa forma que Joule demonstrou que era possível converter trabalho mecânico em energia térmica e extraiu uma relação entre caloria e joule, a unidade criada para homenageá-lo. O trabalho é o equivalente mecânico do calor. A definição moderna de caloria é baseada no joule, e 1 caloria é exatamente 4,186 J, sem relação com a mudança na temperatura da água.
Primeira Lei Termodinâmica e suas Aplicações
Um sistema fechado pode receber ou ceder energia térmica, mas nenhum constituinte pode escapar dele, e nenhum constituinte extra pode ser adicionado. Utilizando os conceitos vistos até aqui, podemos chegar a um enunciado completamente geral da lei da conservação de energia, onde o trabalho e o calor, duas formas de transferência de energia entre um sistema e sua vizinhança, são responsáveis pela alteração da energia do sistema.
Em resumo, para um sistema termodinâmico que só pode ter um único tipo de energia, a energia interna, a lei da conservação pode ser expressa da seguinte forma ∆Eint = Q + W. Onde: Q é o calor transferido entre o sistema e sua vizinhança devido a diferença de temperatura entre eles; W é o trabalho realizado sobre o sistema e ∆Eint é a variação na energia interna do sistema.
A energia interna varia sempre que energia é transferida para dentro ou para fora do sistema como calor ou trabalho. De modo mais formal, podemos escrever a primeira lei da termodinâmica da seguinte maneira: A variação da energia interna de um sistema é igual à soma do calor trocado pelo sistema e do trabalho realizado por ou sobre o sistema.
Há três processos termodinâmicos especiais para gases ideais, onde um dos termos da primeira lei (∆Eint, Q ou W) é nulo, são estes:
-
Processo Adiabático
Nesse processo, nenhum calor flui quando o estado do sistema se altera. Isso é possível em casos em que o processo ocorre tão rapidamente que não há tempo suficiente para que haja troca de calor, por exemplo. Como em processos adiabáticos Q = 0, a primeira lei da termodinâmica pode ser escrita como ∆Eint = W.
-
Processo Isocórico
É um processo em que o volume se mantém constante e por isso o sistema não pode realizar trabalho W = 0. Esse tipo de processo pode acontecer quando um gás, que está confinado em um recipiente rígido, é aquecido e não pode expandir. O cozimento de alimentos em uma panela de pressão, por exemplo, é um processo isocórico. Nesse caso, a equação da primeira lei fica ∆Eint = Q.
-
Processo Isotérmico
É aquele processo que ocorre a temperatura constante. Como a energia interna de um gás é uma função que depende apenas da temperatura, se a temperatura não varia durante o processo que envolve um gás ideal, ∆T = 0, então ∆Eint = 0. Logo, a equação da primeira lei da termodinâmica será Q = -W. Em outras palavras, qualquer energia que entrar no sistema por calor será transferida para fora do sistema por trabalho.
Importante
A energia interna de um gás ideal depende somente da sua temperatura. Ela não depende da sua pressão ou do seu volume (Halliday, 2017, p. 262).
Tanto o trabalho quanto o calor não são variáveis de estado; ou seja, calor e trabalho não são propriedades do sistema e não o caracterizam.
Um fato surpreendente, mas totalmente possível, ocorre durante uma compressão adiabática, onde podemos aumentar a temperatura do sistema sem fornecer calor a ele, ou seja, ∆T é diferente de ∆Q. O trabalho realizado sobre o gás aumenta sua energia interna.
Há ainda dois casos especiais de processos que merecem nossa atenção: os processos cíclicos e a expansão livre. Como foi visto, um processo cíclico envolve uma sucessão de operações que levam o sistema de volta ao seu estado inicial. Podemos ver um exemplo, na figura abaixo, de três processos que começam e terminam no ponto A. Em um ciclo, a variação da energia interna é nula; então, de acordo com a primeira lei Q + W = 0 (processo cíclico).
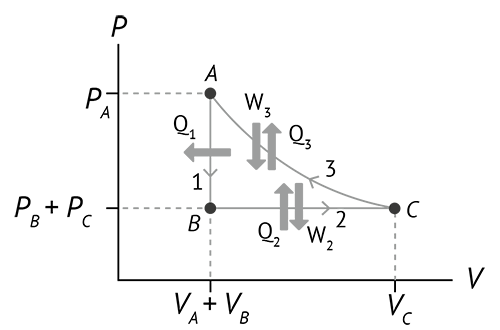
Figura 11: Processo cíclico. Fonte: Halliday (2017, p. 267).
O outro processo é chamado de expansão livre, que ocorre quando um gás inicialmente está dentro de uma das partes do recipiente, ilustrado na figura abaixo, e, quando a válvula é aberta, o gás se expande e começa a preencher o novo volume, referente à outra metade do recipiente previamente evacuado. Na expansão livre, pesos não podem ser levantados, pois nenhum trabalho é realizado. Como o recipiente é isolado, o processo é adiabático. Sendo assim, como W = 0 e Q = 0, a primeira lei da termodinâmica fornece ∆Eint = 0 (Expansão livre).
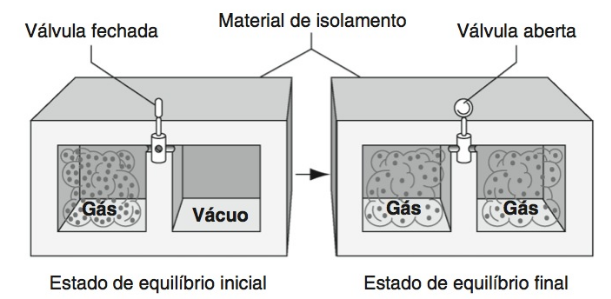
Figura 12: Recipiente onde está ocorrendo expansão livre. Fonte: Halliday (2017, p. 267).
Na expansão livre, a energia interna de um gás ideal permanece constante e, como a energia interna de um gás depende apenas da temperatura, a temperatura também deve se manter constante. A tabela abaixo expõe as aplicações da primeira lei aplicada a gases ideais, relacionada aos diferentes processos e possíveis restrições.
| Processos | Restrições | Primeira Lei |
| Todos | Nenhuma | ∆Eint = Q + W |
| Adiabático | Q = 0 | ∆Eint = W |
| Isocórico | W = 0 | ∆Eint = Q |
| Isobárico | ∆P = 0 | ∆Eint = Q + W |
| Isotérmico | ∆Eint = 0 | Q = - W |
| Cíclico | ∆Eint = 0 | Q = - W |
| Expansão Livre | Q = W = 0 | ∆Eint = 0 |
Tabela 1: Aplicações da primeira lei da termodinâmica. Fonte: Halliday (2017, p. 268).
Imagine que um gás ideal recebe 300 J de calor e realiza uma expansão volumétrica enquanto sua temperatura aumenta. Sabendo que o volume inicial do gás foi de 5 m³ para 11 m³ e que a pressão se manteve constante em 10 Pa, qual foi a variação da energia interna do gás?
Primeiramente, vamos calcular o trabalho realizado pelo sistema:
W = P . ∆V = P (Vf – Vi) = 10 . (11 – 5)
W = 10 . 6 = 60 J
Agora, vamos utilizar a primeira lei da termodinâmica para calcular a variação da energia interna:
∆Eint = Q + W = 300 – 60 = 240 J
A variação da energia interna do sistema foi de 240 J.
Neste tema, vimos como a energia pode ser transferida entre um sistema e sua vizinhança por meio de calor ou trabalho. Enquanto o calor é a transferência de energia térmica entre o sistema e seu entorno, devido à diferença de temperatura entre eles, o trabalho é a transferência de energia que ocorre porque uma força resultante é exercida sobre o sistema. Abordamos que o trabalho realizado pelo gás em uma compressão é negativo, enquanto o trabalho realizado pelo gás em uma expansão é positivo. Ao considerarmos o trabalho realizado pelo ambiente, esses sinais se invertem.
Observamos uma equação central para a termodinâmica que calcula o trabalho realizado por um sistema em um processo isobárico e constatamos que, em um processo que ocorre a volume constante, o trabalho realizado pelo (ou sobre) sistema é nulo. Quando o gás sofre compressão, a energia é transferida da vizinhança para o gás, mas, quando o gás sofre expansão, a energia é transferida do gás para a vizinhança. Por fim, com a primeira lei da termodinâmica, mencionamos um enunciado generalizado da lei da conservação de energia, onde demonstramos que tanto o calor quanto o trabalho podem ser convertidos em energia interna sem haver dissipação de energia.
Tema 3 - Segunda Lei da Termodinâmica e Ciclo de Carnot
Neste tema, abordamos a segunda lei da termodinâmica. A primeira lei é uma afirmação da conservação de energia que garante que uma mudança na energia interna de um sistema pode ocorrer devido à transferência de energia por calor, por trabalho ou por ambos. Embora essa lei seja de grande importância para a termodinâmica, não é capaz de distinguir os processos que ocorrem espontaneamente ou não, e vale ressaltar que, na natureza, ocorrem apenas certos tipos de processos de transformação e transferência de energia.
Veremos que a segunda lei da termodinâmica determina quais processos ocorrem de forma espontânea, ou não, e descobriremos a razão desse enunciado ser um dos mais poderosos e abrangentes da ciência. Também expressaremos essa lei a partir de um conceito chamado entropia. A seguir, examinaremos as máquinas térmicas, dispositivos que convertem energia térmica em energia mecânica e que são governados pela segunda lei. Finalmente, investigaremos a máquina de Carnot, um dispositivo idealizado que nos serve de comparação e nos permite investigar o desempenho das demais máquinas térmicas e sua viabilidade.
Processos Reversíveis e Irreversíveis - Entropia
A primeira lei da termodinâmica, que é fundamentada na lei da conservação de energia, nos revela que a energia interna de um sistema pode variar por conta de uma transferência de calor e/ou trabalho. A questão é que a primeira lei não aborda nenhuma restrição acerca das direções dos fluxos de calor e trabalho; ou seja, em um ciclo termodinâmico, se uma quantidade de calor for cedida pelo sistema e uma quantidade igual de trabalho for recebida pelo sistema, a primeira lei será satisfeita da mesma forma que em um ciclo em que essas transferências ocorrem em sentido oposto.
O que a experiência nos revela é que, embora um ciclo não viole a primeira lei, isso não assegura que esse ciclo realmente possa ocorrer, e foi exatamente esse tipo de experimento que motivou o desenvolvimento da segunda lei da termodinâmica. Sendo assim, para que um ciclo possa ocorrer, ele precisa satisfazer tanto a primeira quanto a segunda lei da termodinâmica. Alguns fenômenos que não são possíveis de acontecer espontaneamente podem nos ajudar a iniciar nossa discussão sobre a necessidade de uma segunda lei.
Um líquido quente em repouso em um recipiente não pode liberar energia térmica interna e começar a girar espontaneamente; da mesma forma, uma quantidade de água não pode, espontaneamente, transformar-se em um cubo de gelo. Embora essas situações não possam acontecer nunca, normalmente podem ser vistas facilmente ocorrendo no sentido inverso. Isso nos leva a uma propriedade na qual raramente pensamos: “Todos os processos naturais ocorrem em apenas um sentido. Estes processos nunca, por meios naturais, ocorrerão em sentido contrário” (Halliday, 2017, p. 280).
A segunda lei da termodinâmica tratará, então, dos sentidos em que os processos podem ocorrer. Basicamente, todos os processos termodinâmicos reais são irreversíveis, mas, para fins de estudo, vários processos reversíveis idealizados podem ser propostos. Em um processo reversível, o sistema está sempre próximo do equilíbrio termodinâmico, e bastaria realizar uma pequena mudança no estado do sistema para poder reverter qualquer mudança nas variáveis termodinâmicas do sistema.
Exemplo
Um disco de gelo a 0°C é colocado em uma lata metálica também a 0°C. Se a temperatura da lata aumentasse levemente, o gelo derreteria e se transformaria em água. Mas, a redução da temperatura da lata faria a água congelar e virar gelo novamente, e o sistema retornaria ao seu estado inicial.
Os processos reversíveis podem ser entendidos como processos em que o sistema sempre está em equilíbrio térmico e é exatamente por isso que um processo reversível é idealizado, pois, se um sistema está em equilíbrio, não haverá troca de calor, e nenhum trabalho seria realizado pelo sistema. O que poderíamos ter é um processo quase reversível em que o sistema seria mantido próximo ao equilíbrio térmico com pequenos ajustes de temperatura e pressão. Por outro lado, há processos termodinâmicos que não podem ser desfeitos, e durante esses processos, o sistema não está em equilíbrio.
Vamos examinar alguns exemplos:
-
Caso 1
Ao abandonar uma pedra de uma determinada altura, medida em relação ao solo, ela cai. Já uma pedra que se encontra em repouso sobre o solo jamais, espontaneamente, subirá pelo ar.
-
Caso 2
Ao pingar uma gota de tinta sobre um recipiente com água, as moléculas da tinta se espalharão pelo volume de água. E sabemos que, por conta própria, essas moléculas nunca se reagruparão e tornar-se-ão uma gota novamente.
Isso nos leva à conclusão de que processos espontâneos, que ocorrem apenas em um único sentido, são irreversíveis. De forma simplificada, esses processos não podem ser revertidos por meio de pequenas alterações no ambiente onde ocorrem. A expansão livre, por exemplo, é um tipo de processo irreversível.
Em essência, todos os processos naturais são irreversíveis.
Note que, mesmo que esses exemplos de processos impossíveis acontecessem, não violariam a lei da conservação de energia. Vamos considerar novamente o exemplo dado no caso 1. A pedra sobre o solo poderia receber energia térmica dele; essa energia poderia ser convertida em energia cinética e arremessar a pedra para cima. Contudo, isso não acontece. Isso significa que não é a energia que controla o sentido em que o processo ocorre, e sim uma outra propriedade do sistema chamada entropia, representada pela letra S.
A propriedade central da entropia, chamada de princípio da entropia, é: “Se um processo irreversível ocorre em um sistema fechado, a entropia deste sistema sempre aumenta; ela nunca decresce." Deste modo, a entropia é diferente da energia, já que não obedece a uma lei de conservação. Em um sistema fechado, sua energia permanecerá constante, independentemente das transformações sofridas; já a entropia, em processos irreversíveis, sempre aumentará.
Nosso interesse está na variação da entropia, ou seja, em ∆S, e não em S. Em um sistema fechado em que ocorre um processo irreversível, ∆S > 0. Se esse processo pudesse acontecer no sentido inverso, a variação da entropia seria negativa, ∆S < 0, o que violaria o princípio da entropia.
Vamos definir a variação de entropia ∆S que ocorre em um sistema fechado quando ele passa de um estado inicial para um estado final, ambos bem definidos, por meio de um processo reversível. Nos processos reversíveis, tanto o sistema quanto o ambiente sofrem uma pequena modificação que, quando revertida, faz com que eles retornem às condições iniciais. A definição de entropia para processos reversíveis é:
$\Delta \mathrm{S}=\int_i^f \frac{d Q}{T}$
Onde dQ é o incremento de energia térmica que é transferido do sistema (fechado) ou para o sistema, sob uma temperatura T em kelvin. Observe que a integral é calculada a partir de um estado inicial i do sistema até um estado final f, e que o calor transferido e a temperatura em que ocorre o processo são importantíssimos para a definição de variação de entropia. A unidade de medida da variação de entropia é J/K (joule por kelvin).
Se o processo for isotérmico, isto é, se ocorrer a temperatura constante, a equação da variação da entropia fica reduzida a:
$\Delta \mathrm{S}=\frac{Q}{T}$
Importante
O fato de uma temperatura em kelvin ser sempre positiva implica que a variação da entropia terá o mesmo sinal algébrico do calor. Ou seja, para processos reversíveis em um sistema fechado, se calor é recebido pelo sistema (Q > 0), a entropia aumenta (∆S > 0), e se calor é cedido pelo sistema (Q < 0), a entropia diminui (∆S < 0).
Se a equação para o cálculo da variação da entropia só pode ser utilizada em processos reversíveis, que são uma idealização, como fazer para calcular essa variação em processos reais (irreversíveis)? Como a entropia é uma propriedade de estado, quando um sistema fechado passa de um estado inicial i para um estado final f, a variação na entropia depende apenas das propriedades desses dois estados. A variação não depende de nada que interligue esses dois estados e nem mesmo do fato de o processo ser reversível ou irreversível.
Desse modo, podemos calcular a variação da entropia em um processo irreversível de um sistema que passa de um estado inicial i para um estado final f da seguinte forma:
Em resumo, esta análise acerca da variação da entropia resultou na primeira forma de enunciar a segunda lei: quando um sistema fechado sofre mudanças, sua entropia nunca diminui. Se o processo for irreversível, a entropia aumenta, e se o processo for reversível, a entropia se mantém constante.
Máquinas Térmicas, 2ª Lei da Termodinâmica e Refrigeradores
Uma máquina térmica é um dispositivo desenvolvido para retirar energia em forma de calor do seu ambiente e convertê-la em trabalho, ou seja, que transforma energia em trabalho útil. Esses dispositivos operam utilizando uma substância de trabalho. Um motor de automóvel, por exemplo, tem como substância de trabalho uma mistura de ar com gasolina. Outro detalhe importante é que, para que a máquina opere de forma autossustentada, precisa operar em ciclo fechado, ou seja, retornando sempre a um estado inicial arbitrário.
Em termos simplificados, um dispositivo que trabalha em ciclo fechado retorna às suas condições iniciais periodicamente. A máquina térmica carrega a substância de trabalho por um processo cíclico na seguinte sequência: a substância de trabalho absorve calor de um reservatório de energia em alta temperatura, a fonte quente, o trabalho é realizado pelo motor, e a energia que sobra é rejeitada como calor para um reservatório em temperatura mais baixa, a fonte fria (ou sorvedouro).
Um reservatório térmico é um corpo que, mesmo que sofra transferências de calor, mantém sua temperatura sempre constante.
Como uma máquina térmica opera em ciclo, sua temperatura e a energia térmica retornam a seus valores iniciais no término de cada ciclo; logo, não há uma variação resultante de energia térmica: ∆Ures = 0. Uma máquina térmica representada de forma simples e bastante útil está ilustrada na figura abaixo, onde Qq é a energia que entra na máquina (calor recebido da fonte quente), W é o trabalho realizado pela máquina, e Qf é a energia que sai da máquina. A máquina realiza trabalho W; logo, um trabalho negativo seria aquele realizado sobre a máquina.
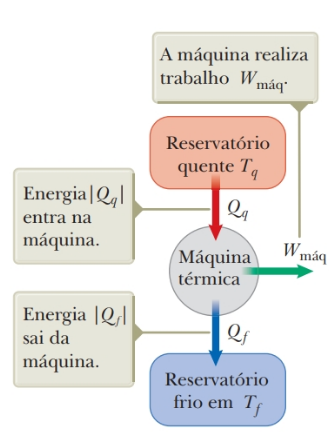
Figura 13: Representação de uma máquina térmica. Fonte: Jewett Jr. (2013, p. 191).
Utilizaremos em nossa abordagem matemática da máquina térmica valores absolutos para aquelas transferências de energia por calor positivo, e a direção da transferência será indicada com um sinal positivo ou negativo. Como as máquinas térmicas sempre retornam às suas condições iniciais, pois trabalham em ciclos, suas energias iniciais e finais são iguais, o que resulta em uma variação nula da energia interna ∆Eint = 0. Logo, pela primeira lei da termodinâmica (∆Eint = Q + W) temos, Q – W = 0.
O trabalho resultante W, realizado por uma máquina térmica, é igual à energia total resultante (Qtot = Qq – Qf), ou seja:
$W=\left|Q_q\right|-\left|Q_f\right|$
A eficiência térmica de uma máquina térmica, comumente chamada de Rendimento, é dada pela proporção do trabalho realizado pela energia recebida da fonte quente:
$\epsilon=\frac{w}{Q q}$
Ou ainda:
$\epsilon=\frac{\left|Q_q\right|-\left|Q_f\right|}{Q q}=1-\frac{\left|Q_f\right|}{\left|Q_q\right|}$
Exemplo: Uma máquina térmica recebe 2500J de energia de um reservatório quente durante um ciclo, rejeitando 1000J para o reservatório frio. Calcule a eficiência da máquina e o trabalho realizado por ela.
Primeiramente, aplicaremos a equação da eficiência em função das quantidades de calor Qq e Qf:
$\epsilon=1-\frac{\left|Q_f\right|}{\left|Q_q\right|}=1-\frac{|1000|}{|2500|}=1-0,4=0,6 \times 100 \%=60 \%$
O valor da eficiência pode ser multiplicado por 100%, conforme mostra o exemplo, para que seja expressa em porcentagem. Agora, basta calcular o trabalho:
$W=\left|Q_q\right|-\left|Q_f\right|=2500-1000=1500 \mathrm{~J}$
Vimos que a primeira lei da termodinâmica diz que a energia interna de um sistema pode variar como consequência de transferências de calor e trabalho. Ou seja, um copo com água que esfria sobre a mesa obedece à primeira lei. Entretanto, foi necessário estabelecer uma segunda lei, que impõe limitações à quantidade e também ao sentido de transferências de energia térmica entre sistemas. A segunda lei também determina as possíveis eficiências das máquinas térmicas.
Enquanto o experimento de Joule demonstrou que trabalho pode ser convertido em calor, experimentos mostram que é impossível construir uma máquina térmica que, operando em ciclos, possa converter todo o calor recebido em trabalho. Em outras palavras, é impossível que uma máquina térmica possua eficiência de 100%.
Essa expressão da segunda lei, já vista anteriormente, uma vez que a primeira foi em termos da entropia, é conhecida como o enunciado de Kelvin-Planck da segunda lei da termodinâmica, que, em termos mais formais:
É impossível que um sistema seja submetido a um processo em que absorva calor de um reservatório térmico a uma determinada temperatura e converta esse calor completamente em trabalho mecânico sem ceder calor para um reservatório térmico com temperatura mais baixa (Bauer, 2012, p.274)
Em uma máquina térmica, a transferência de calor ocorre do corpo de maior temperatura em direção ao de menor temperatura, pois essa é a direção natural. É bem provável que em sua residência haja um refrigerador ou um ar-condicionado, que são dispositivos que operam fazendo com que o ar interno, que é mais frio do que o ar externo, fique ainda mais frio. Mas isso não viola a segunda lei da termodinâmica? Na verdade, não! O que a segunda lei afirma é que o calor não pode ser transferido de um objeto mais frio para um objeto mais quente de modo espontâneo. Os aparelhos que desempenham essa função são conhecidos como refrigeradores, como as geladeiras domésticas, ou bombas de calor, como o ar-condicionado. A função desempenhada por esses dispositivos não ocorre de forma espontânea, mas de modo assistido e necessita de energia elétrica.
Os refrigeradores e bombas de calor, apontados na figura abaixo, recebem energia Qf da fonte fria e rejeita energia para a fonte quente Qq e isso só pode ocorrer se for realizado trabalho sobre o motor. Conforme a primeira lei indica, a energia rejeitada para a fonte quente deve ser igual à soma do trabalho realizado com a energia recebida da fonte fria.
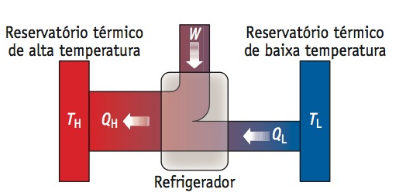
Figura 14: Diagrama de fluxo de um refrigerador que opera entre dois reservatórios térmicos. Fonte: Bauer (2012, p. 243).
Sendo assim, um ar-condicionado ou geladeira, por exemplo, para manter o ar frio, remove continuamente calor do reservatório frio e rejeita calor para a cozinha ou para o exterior. O que se deseja, na prática, é que esse processo se conduza com um trabalho mínimo. Se possível, até mesmo sem realizar qualquer trabalho, mas isso violaria a segunda lei da termodinâmica expressa em sua terceira forma pelo enunciado de Clausius, que diz que não é possível construir uma máquina que opere segundo um ciclo e cujo único efeito seja transferir energia continuamente, em forma de calor, de um corpo para outro de temperatura mais alta, sem que haja entrada de energia por trabalho. Em outras palavras, como a energia não flui espontaneamente em forma de calor de um corpo “frio” para um corpo “quente”, é necessário que haja a entrada de trabalho para que o dispositivo funcione.
Importante
Embora os enunciados de Clausius e de Kelvin-Planck sobre a segunda lei da termodinâmica pareçam não ter relação entre si, na realidade, são equivalentes em todos os aspectos. Se uma das afirmativas é falsa, a outra também é.
Como os refrigeradores e bombas de calor operam em ciclo, ∆Eint = 0, e a primeira lei da termodinâmica exige que:
$Q_q+Q_f=W_{\text {entrada }}$
Como é descrita em termos de um número chamado coeficiente de desempenho (K), d é desejado que o refrigerador retire o máximo de calor possível do reservatório mais frio, Qf, a sua eficiência ado em função de Qf e W, que é o trabalho realizado no refrigerador, definido por:
$\mathrm{K}=\frac{Q_f}{w}$
Um bom refrigerador deve ter deve ter coeficiente de desempenho alto, entre 5 e 6.
Há ainda uma terceira lei da termodinâmica, formulada no início do século XX por W. H. Nernst e Max Planck. A terceira lei trata da entropia de sistemas que estão na temperatura de zero absoluto e determina que, nessa condição, a entropia do sistema é zero.
Máquina de Carnot
No ano de 1824, o engenheiro Sadi Carnot descreveu uma máquina teórica de muita relevância prática e teórica, que ficou conhecida como Máquina de Carnot. Carnot mostrou que uma máquina térmica que opera entre dois reservatórios térmicos, em um ciclo ideal, reversível, conhecido como ciclo de Carnot, é a máquina de maior eficiência possível. Com isso, a máquina de Carnot estabelece um limite de eficiência superior para as demais máquinas térmicas.
Em outras palavras, nenhuma máquina térmica pode obter eficiência maior que uma máquina que opera segundo o ciclo de Carnot. O teorema de Carnot pode ser definido como: uma máquina térmica real que opera entre dois reservatórios térmicos não pode ter eficiência maior que uma máquina de Carnot que opera entre os mesmos reservatórios.
Podemos ver na figura a seguir um diagrama PV, que mostra que um ciclo de Carnot consiste em dois processos isotérmicos e dois adiabáticos. Para compreender os processos do ciclo de Carnot, vamos escolher um ponto 1, onde o ciclo se inicia. A princípio, o sistema passa por um processo isotérmico com temperatura TH = 400 K e se expande. Já no ponto 2, se inicia uma expansão adiabática, sem transferência de calor.
No ponto 3, se inicia novamente um processo isotérmico com temperatura TL = 300 K e o sistema sofre compressão. Por fim, no ponto 4, o sistema passa por um segundo processo adiabático e o ciclo é completado quando o sistema retorna ao ponto 1.
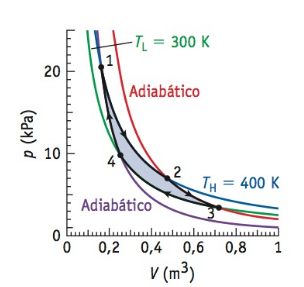
Figura 15: Ciclo de Carnot. Fonte: Bauer (2012, p. 244).
O que torna a máquina de Carnot a mais eficiente de todas as máquinas é uma característica única que possui: sua reversibilidade. A máquina de Carnot é capaz de operar inversamente, ou seja, como uma bomba de calor. As máquinas reais são menos eficientes, pois, além de não operar com um ciclo reversível, ainda sofrem perdas por atrito e por condução.
Embora a eficiência de uma máquina de Carnot seja a máxima possível, ela não pode atingir 100%, pois violaria a segunda lei da termodinâmica. Essa eficiência é dada por:
$\epsilon=1-\frac{T_f}{T q}$
Onde Tf é a temperatura da fonte fria e Tq é a temperatura da fonte quente. Observe que a eficiência de uma máquina de Carnot depende apenas da razão entre as temperaturas da fonte fria e da fonte quente.
Observe o cálculo da eficiência da máquina de Carnot cujo ciclo foi ilustrado na figura acima:
$\begin{aligned} & \epsilon=1-\frac{T_f}{T q}=1-\frac{300}{400}=1-0,75 \\ & \epsilon=0,25 \times 100 \%=25 \%\end{aligned}$
Neste tema, vimos a primeira lei da termodinâmica, uma expressão da lei da conservação de energia, que diz que a variação da energia de um sistema pode ser alterada por meio de transferências de energia, como calor, trabalho ou ambos. Abordamos os tipos de processos, reversíveis e irreversíveis, e o conceito de entropia, que diz que, se um processo irreversível ocorre em um sistema fechado, a entropia deste sistema sempre aumenta, e que, se o processo for reversível, a entropia se mantém constante.
Mencionamos a segunda lei da termodinâmica e suas três formas de enunciados, que, em suma, determinam um sentido para as transferências de energia que ocorrem espontaneamente e também limitam a eficiência de máquinas térmicas. Analisamos a eficiência das máquinas térmicas, dos refrigeradores e bombas de calor. Por fim, discutimos a respeito de uma máquina térmica idealizada, chamada de máquina de Carnot, que opera em um ciclo denominado ciclo de Carnot, e é a máquina térmica que possui a maior eficiência entre as máquinas, mas que ainda assim não possui rendimento de 100%, obedecendo à segunda lei.
Além da Sala de Aula
Na leitura indicada, o autor aborda o fato de que, até aproximadamente 1850, as áreas da Termodinâmica e da Mecânica eram consideradas duas áreas distintas da ciência. O princípio da conservação da energia parecia servir apenas para descrever alguns tipos de sistemas mecânicos, mas experiências realizadas em meados do século XIX pelo cientista inglês James Joule e por outros mostraram uma conexão entre a transferência de energia por calor em processos térmicos e a transferência de energia por trabalho em processos mecânicos.
Atualmente, sabe-se que a energia mecânica pode ser transformada em energia interna, o que é fortemente abordado pelo autor. Aqui, é feita uma explicação detalhada da primeira lei da termodinâmica, com exemplos de algumas de suas aplicações mais importantes. O autor explica que a primeira lei da termodinâmica descreve sistemas nos quais a única alteração que ocorre na energia é aquela da energia interna, em que as transferências de energia ocorrem por calor e trabalho.
Todos estes pontos são tratados por Jewett Jr. e Serway (2013). Por isso, faça a leitura da página 142 a 149 do livro Física para Cientistas e Engenheiros: Oscilações; Ondas e Termodinâmica, disponível na Minha Biblioteca.
Lembre-se de que para iniciar a leitura do livro sinalizado, é necessário fazer login na Minha Biblioteca.
Título do livro/artigo: Trabalho e Calor em Processos Termodinâmicos
Páginas indicadas: 142 a 149
Referência: JEWETT JR., John W.; SERWAY, Raymond A. Física para Cientistas e Engenheiros: Volume 2: Oscilações; Ondas e Termodinâmica. São Paulo: Cengage Learning, 2017. E-book. ISBN 9788522127092.
Na leitura indicada, o autor aborda o conceito de reservatório térmico, que pode ser de dois tipos: um comumente chamado de fonte, do qual se transfere calor, e o outro, de sorvedouro, para onde se transfere calor. Feito isso, trata de dois enunciados clássicos da segunda lei: o enunciado de Kelvin-Planck e o enunciado de Clausius. Esses enunciados servirão de base para a discussão sobre motores térmicos.
O autor ainda explica que motores térmicos, refrigeradores e bombas de calor são dispositivos de conversão de energia, transformando quantidades de energia entre Q e W com diferentes direções de conversão. Por fim, os processos reversíveis e irreversíveis são explicados de forma objetiva e por meio de diversos exemplos práticos, assim como os fatores que tornam um processo irreversível.
Todos estes pontos são tratados por Borgnakke e Sonntag (2018). Por isso, faça a leitura da página 209 a 215 do livro Fundamentos da termodinâmica, disponível na Minha Biblioteca.
Lembre-se de que para iniciar a leitura do livro sinalizado, é necessário fazer login na Minha Biblioteca.
Título do livro/artigo: Fundamentos da Termodinâmica
Páginas indicadas: 209 a 215
Referência: BORGNAKKE, Claus; SONNTAG, Richard E. Fundamentos da termodinâmica. São Paulo: Editora Blucher, 2018. E-book. ISBN 9788521207931.
Rendimento de uma Caldeira
Neste estudo de caso, analisaremos o rendimento de uma caldeira, um tipo de máquina térmica utilizada em uma usina sucroalcooleira, responsável por produzir derivados da cana, como açúcar, por exemplo. Nessa máquina térmica, o combustível utilizado, ou seja, a substância de trabalho, é o próprio bagaço da cana, que tem como finalidade a geração de energia para a produção do vapor.
Considere a seguinte situação:
No atual cenário global, há uma preocupação de que o desenvolvimento ocorra de forma sustentável, o que é um grande desafio. Diante disso, a geração de energia feita de modo limpo e eficiente impacta de forma positiva tanto o meio ambiente quanto as relações econômicas industriais. Uma alternativa energética importante é a biomassa, que reaproveita recursos naturais renováveis. O bagaço de cana tem sido uma matéria-prima bastante explorada, utilizado como combustível para gerar energia térmica, mecânica e elétrica para produzir vapor.
As caldeiras aquatubulares, que são um trocador de calor, destacam-se entre os geradores de vapor. Essa máquina térmica opera com pressão superior à atmosférica, produzindo vapor através de energia térmica fornecida por uma fonte quente. Uma usina sucroalcooleira precisa avaliar a eficiência e as perdas de calor de sua caldeira aquatubular, que utiliza o bagaço da cana como combustível. A caldeira recebe da fonte quente 721,25 . 106 KJ de energia e realiza um trabalho de 490,45 . 106 KJ.
Questionamentos para reflexão:
- Qual é a perda de energia em forma de calor nessa caldeira?
- É possível ter uma boa eficiência utilizando esse combustível sustentável?
- Qual seria a eficiência de uma máquina de Carnot operando entre os mesmos reservatórios térmicos?
- A energia gerada nessa usina viola a segunda lei da termodinâmica?
Assista às videoaulas a seguir, que têm como objetivo reforçar os conteúdos abordados nesta unidade de maneira didática para embasar os conceitos e teorias trabalhados. Esperamos que contribuam significativamente para seu aprendizado e que a busca pelo conhecimento não se encerre neste percurso de aprendizagem.
Neste infográfico, veremos as três leis da termodinâmica: a lei zero, que trata do equilíbrio térmico entre os corpos; a primeira lei, que aborda a variação da energia interna relacionada às transferências de calor e trabalho; e a segunda lei, que impõe restrições sobre o sentido em que as trocas de calor podem ocorrer e limita a construção de uma máquina térmica.

Nesta unidade, discutimos o que são fases e estados da matéria, além de propriedades intensivas e extensivas de um sistema. Definimos o conceito de equilíbrio termodinâmico e de quase equilíbrio a fim de descrever o estado de um sistema durante um processo. Analisamos a definição da lei zero da termodinâmica e vimos como foi fundamental para a compreensão do que é medida de temperatura e o equilíbrio térmico.
Abordamos que um sistema pode transferir energia para sua vizinhança tanto em forma de calor quanto de trabalho, e que o trabalho é o equivalente mecânico do calor. Contudo, o experimento de Joule mostrou que é possível até mesmo converter trabalho em calor. A primeira lei da termodinâmica afirma que calor e trabalho são responsáveis pela variação de energia interna de um sistema e se aplica a processos termodinâmicos isobáricos, isotérmicos, isocóricos, adiabáticos, cíclicos e também para a expansão livre.
Analisamos a segunda lei da termodinâmica, que estabelece, sem violar a primeira lei, os sentidos nos quais as transferências de calor e trabalho devem ocorrer em processos espontâneos. A segunda lei é enunciada de três formas: uma relacionada à variação da entropia do sistema, outra limitando a eficiência das máquinas térmicas e, por fim, a terceira limitando o funcionamento dos refrigeradores. Aplicamos equações de eficiência para medir o rendimento das máquinas térmicas e refrigeradores e conhecemos a máquina de Carnot.
Para sua autorreflexão:
- Relacionou os conceitos de equilíbrio térmico com a Lei Zero da Termodinâmica?
- Reconheceu a relação entre trabalho e calor em sistemas macroscópicos?
- Utilizou a equação do trabalho para processos isobáricos?
- Identificou a primeira e segunda lei da termodinâmica?
- Reconheceu a importância do cálculo do rendimento de diferentes máquinas térmicas?
BAUER, Wolfgang; WESTFALL, Gary D.; DIAS, Helio. Física para Universitários. Porto Alegre: AMGH, 2012. E-book. ISBN 9788580551600. Disponível em: https://integrada.minhabiblioteca.com.br/reader/books/9788580551600/. Acesso em: 03 dez. 2024.
BORGNAKKE, Claus; SONNTAG, Richard E. Fundamentos da termodinâmica. São Paulo: Editora Blucher, 2018. E-book. ISBN 9788521207931. Disponível em: https://integrada.minhabiblioteca.com.br/reader/books/9788521207931/. Acesso em: 03 dez. 2024.
HALLIDAY, David; RESNICK, Robert; KRANE, Kenneth S. Física, v. 2. 5. ed. Rio de Janeiro: LTC, 2017. E-book. ISBN 978-85-216-1946-8. Disponível em: https://integrada.minhabiblioteca.com.br/reader/books/978-85-216-1946-8. Acesso em: 03 dez. 2024.
JEWETT JR., John W.; SERWAY, Raymond A. Física para Cientistas e Engenheiros: Volume 2: Oscilações; Ondas e Termodinâmica. São Paulo: Cengage Learning, 2017. E-book. ISBN 9788522127092. Disponível em: https://integrada.minhabiblioteca.com.br/reader/books/9788522127092/. Acesso em: 03 dez. 2024.
KNIGHT, Randall D. Física 2: uma abordagem estratégica. 2. ed. Porto Alegre: Bookman, 2009. E-book. ISBN 9788577805389. Disponível em: https://integrada.minhabiblioteca.com.br/reader/books/9788577805389/. Acesso em: 03 dez. 2024.







