Nesta unidade iniciaremos o estudo da hidrostática, uma investigação sobre fluidos em repouso, definindo o conceito de fluido e enunciando alguns princípios gerais sobre gases e líquidos. Conheceremos tambémas grandezas que caracterizam os fluidos, a densidade e a pressão e a distinção entre pressão manométrica, pressão atmosférica e pressão absoluta.
Em seguida, estudaremos como a pressão varia em um fluido em repouso, ou seja, como a pressão aumenta com a profundidade. Perceberemos que a pressão exercida sobre um ponto no interior de um líquido é resultado da soma da pressão atmosférica com a pressão exercida pelo peso da própria coluna de líquido. Analisaremos o princípio de Pascal e como ele se aplica em dispositivos hidráulicos e também o Princípio de Arquimedes, que trata da força que surge sobre corpos imersos em um fluido.
Por fim, estudaremos a dinâmica dos fluidos, que é o estudo de fluidos em movimento, partindo do modelo de fluido ideal. Analisaremos como a mudança no diamêtro de uma tubulação influencia na velocidade de escoamento do fluido e encerraremos com a equação de Bernoulli, que relaciona duas variáveis do fluido, a pressão e a velocidade.
Ao realizar sua leitura, preste atenção às definições de densidade e massa específica, que são ambas a razão entre a massa e o volume. No entanto, observe que a densidade pode variar, enquanto a massa específica é constante, pois é uma característica intrínseca da substância e não do corpo. Note também que a pressão é definida como a força aplicada sobre uma determinada área, e que é possível medir a pressão atmosférica da Terra utilizando um barômetro. Assim, familiarize-se com o funcionamento e a construção deste dispositivo, além de compreender os diferentes tipos de pressão abordados.
Ao explorar o princípio de Pascal, concentre-se na ideia central: a pressão aplicada em um ponto de um fluido é transmitida integralmente a todos os outros pontos desse fluido. Entenda como esse princípio possibilitou a criação de dispositivos como a prensa hidráulica.
No estudo da equação da continuidade, direcione sua atenção para a principal implicação: quanto menor a área disponível para o escoamento de um fluido, maior será sua velocidade. Por fim, compreenda a conclusão da equação de Bernoulli, que estabelece que, quanto maior a velocidade de escoamento de um fluido, menor será a pressão exercida sobre suas fronteiras.
Nos temas a seguir, você irá aprofundar seu conhecimento com o estudo dos assuntos específicos desta unidade e, ao final, deverá atingir os seguintes objetivos de aprendizagem:
- Aplicar o conceito e a equação de massa específica.
- Definir os tipos de pressão e utilizar suas unidades de medida.
- Relacionar o princípio de Arquimedes à flutuação dos corpos.
- Reconhecer e aplicar a equação da continuidade.
- Aplicar a equação de Bernoulli e identificar sua consequência.
Tema 1 - Princípios de Hidrostática
Neste tema, iremos aprofundar nossos conhecimentos em hidrostática, parte da física responsável pelo estudo dos fluidos em repouso e como estes reagem sob a aplicação de uma força. Podemos definir fluido como uma substância capaz de fluir, ou seja, escoar. Devido a esta propriedade, um fluido pode assumir a forma do recipiente que o contém, em outras palavras, um fluido não possui forma própria.
Um fluido é um sistema macroscópico formado por um grande número de partículas. São exemplos de fluidos os gases e os líquidos, sendo este último nosso objeto de interesse. Os gases possuem moléculas distanciadas entre si, o que os torna compressíveis; seu volume pode aumentar ou diminuir. Já os líquidos, por conta de seu arranjo molecular, com moléculas bem próximas umas das outras, são praticamente incompressíveis. Como consequência disso, ao colocar um gás em um recipiente, ele irá expandir e ocupar o volume total do recipiente. Mas, ao colocar um líquido em um recipiente, ele ocupará apenas o volume correspondente ao seu volume inicial. A força de ligação entre as moléculas do líquido as mantém tão perto quanto podem estar, mas não é capaz de impedir o escorregamento entre elas.
Massa Específica ou Densidade
Um sistema macroscópico, como um fluido, por exemplo, pode ser caracterizado por seu volume V, que é basicamente o espaço ocupado por ele. São diversas as unidades de medida de volume utilizadas, sendo cm3, m3 e litros (L) as mais comuns.
Em nossos cálculos, será necessário convertê-las para m3, que é a unidade do SI (sistema internacional). A Figura 1 é um esquema que demonstra os modos de conversão de unidades de volume:
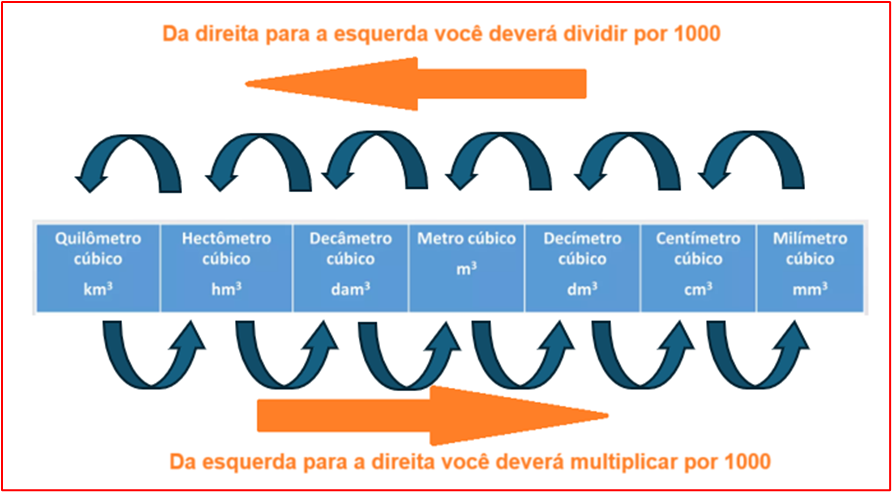
Figura 1: Esquema de conversões de unidades. Fonte: Elaborada pela autora.
Para fazer a conversão entre L (litros) e m3, pode-se utilizar a seguinte relação:
1000L = 1m3
A massa específica, representada pela letra ρ, também é um parâmetro utilizado para caracterizar um sistema e pode ser definida como a razão entre a quantidade de massa de uma substância pelo volume ocupado por ela. A massa específica, ou densidade, é então dada pela seguinte expressão matemática:
Importante
A unidade de medida da massa específica no SI é kg/m3, mas a unidade g/cm3 também é largamente utilizada. É necessário atenção, pois em muitos cálculos será necessário converter a unidade de g/cm3 para kg/m3 realizando a conversão de gramas para quilogramas e de centímetros cúbicos para metros cúbicos. Para facilitar esse processo, pode-se utilizar o seguinte fator de conversão:
1 g/cm3 = 1000 kg/m3.
Ou seja, basta multiplicar por 1000 para converter de 1 g/cm3 para 1000 kg/m3.
A seguir, temos um exemplo de cálculo de densidade:
Um certo líquido de massa igual a 8 g ocupa um volume de 10 cm3. Calcule a densidade desse líquido em kg/m3.
Nesse caso, iremos, primeiramente, aplicar a equação de cálculo de densidade e substituiremos os valores de massa e volume dados no enunciado do problema:
$\begin{aligned} \rho & =\frac{m}{v} \\ \rho=\frac{8}{10} & =0,8 \frac{\mathrm{~g}}{\mathrm{~cm}^3}\end{aligned}$
Agora, realizaremos a transformação da unidade de medida multiplicando por 1000:
$\rho=0,8 \frac{\mathrm{~g}}{\mathrm{~cm}^3} \cdot 1000=800 \frac{\mathrm{~kg}}{\mathrm{~m}^3}$
A temperatura e a pressão podem influenciar na densidade dos corpos. A Tabela 1 e a Tabela 2 trazem os valores de densidade, em kg/m3, de importantes substâncias puras à temperatura de 0oC e pressão de 1 atm.
|
SÓLIDOS |
|
|
Alumínio |
2,70.103 |
|
Cobre |
8,90.103 |
|
Cortiça |
0,24.103 |
|
Chumbo |
11,30.103 |
|
Ferro |
7,80.103 |
|
Gelo |
0,92.103 |
|
Isopor |
0,10.103 |
|
Ouro |
19,30.103 |
|
Prata |
10,50.103 |
|
Platina |
21,40.103 |
Tabela 1: Densidade de sólidos em kg/m3. Fonte: Telles; Mongelli Netto (2013, p.124).
|
LÍQUIDOS |
|
|
Água |
1,00 |
|
Água do mar |
1,03 |
|
Álcool etílico |
0,81 |
|
Mercúrio |
13,60 |
|
Óleo de Oliva |
0,92 |
|
GASES |
|
|
Ar |
1,29 |
|
Gás carbônico |
1,98 |
|
Hélio |
0,18 |
|
Hidrogênio |
0,09 |
|
Oxigênio |
1,43 |
Tabela 2: Densidade de líquidos e gases em kg/m3. Fonte: Telles; Mongelli Netto (2013, p.124).
Importante
Tanto a massa específica quanto a densidade são definidas como a razão entre massa e volume. Entretanto, há uma diferença entre os dois conceitos: enquanto a densidade é uma característica de um corpo e pode variar, a massa específica é uma característica de uma substância, sendo, por isso, constante. No estudo dos fluidos, consideraremos os dois conceitos como equivalentes.
A densidade é um dos fatores que influencia a flutuabilidade de um corpo em um líquido. Para que haja flutuação, é necessário que o corpo tenha uma densidade inferior à densidade do líquido onde está imerso.
Exemplo
Se colocarmos uma rolha de cortiça em um aquário cheio de água, ela flutuará, pois a densidade da cortiça, cerca de 0,24 g/cm3, é bem inferior à densidade da água, que é de 1 g/cm3, como percebemos a seguir:

Ao colocarmos líquidos imiscíveis (aqueles que não se misturam) dentro de um recipiente, após atingirem o equilíbrio, percebemos que o líquido mais denso se localiza no fundo do recipiente, enquanto o menos denso fica acima. Esse fenômeno pode ser percebido facilmente em nosso cotidiano: basta acrescentar delicadamente em um recipiente, água e óleo; em alguns instantes a mistura estará em equilíbrio e será possível perceber claramente que o óleo, por ser menos denso que a água, se localizará na parte superior do recipiente, enquanto a água irá para o fundo.

Figura 2: Mistura de água e óleo. Fonte: Dreamstime.
Pressão
A habilidade de escoamento de um fluido impede que um líquido consiga sustentar uma força paralela à sua superfície. Assim, em fluidos em repouso, a única força relevante é aquela que atua perpendicularmente à superfície do fluido, chamada de força normal.
A pressão pode ser definida como a intensidade da força normal dividida pela área da superfície onde essa força atua e pode ser expressa a partir da seguinte relação matemática:
$P=\frac{F}{A}$
Importante
A pressão não é uma grandeza vetorial, mas sim uma grandeza escalar.
Como a pressão, por sua definição, possui dimensões de força pela área, sua unidade de medida N/m2, mas, no sistema internacional (SI), sua unidade de medida é Pascal (Pa), definida como:
1 Pa = 1 N/ m2
A Figura 3 mostra como um fluido exerce pressão contra uma pequena área A por meio de uma força, o que faria o líquido jorrar lateralmente caso houvesse um orifício na parede do recipiente, como ilustra a Figura 4.
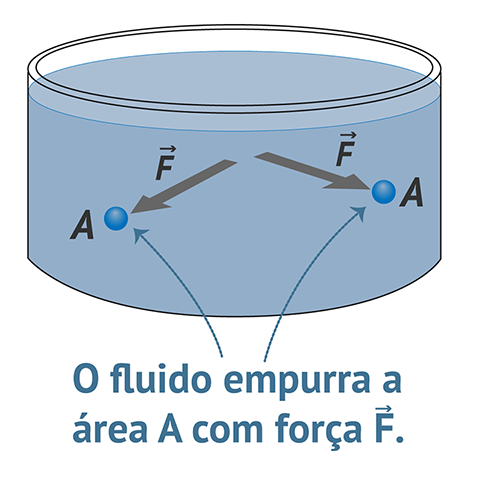
Figura 3: Fluido exercendo pressão nas paredes de um recipiente. Fonte: Adaptada de Knight (2009, p. 26).
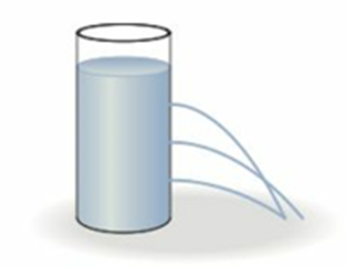
Figura 4: Pressão da água empurrando o líquido. Fonte: Adaptada de Knight (2009, p. 26).
A seguir, temos um exemplo de cálculo de pressão exercida por uma massa de água.
Exemplo
Um vaso de base quadrada de aresta 20 cm, como mostra a figura, é completamente cheio de água, de modo que a água exerce uma força de 40 N no fundo do recipiente.
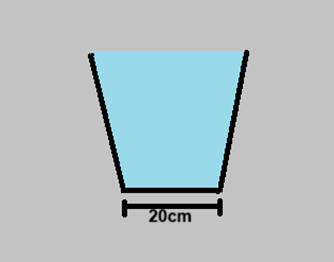
Qual seria a pressão exercida pela coluna de líquido no fundo do recipiente?
Precisamos calcular a área base, mas, antes, iremos transformar a medida da aresta de centímetros para metros, dividindo por cem:
$a=\frac{20}{100}=0,2 m$
Sabendo que a área de uma base quadrada é dada pela aresta ao quadrado, temos:
$A=a^2=0,2 \times 0,2=0,04 m^2$
Aplicando a equação para cálculo de pressão, temos:
$P=\frac{F}{A}=\frac{40}{0,04}=1000 \mathrm{~Pa}$, ou ainda 1 KPa
Note: 1 KPa = 1000 Pa
Princípio de Arquimedes
Arquimedes foi um dos maiores matemáticos, físicos e engenheiros da Grécia Antiga. Viveu aproximadamente entre 287 a.C. e 212 a.C. e é amplamente reconhecido por suas contribuições fundamentais para a matemática e a ciência.

Figura 5: Arquimedes. Fonte: Wikipedia.
A Figura 6 ilustra um volume de um líquido envolvido por um fino saco plástico que está submerso em água. Esse volume de líquido está em equilíbrio estático, ou seja, seu peso, que é uma força vertical apontando para baixo, está sendo equilibrado por uma força de mesma intensidade e direção, apontando para cima. A água em torno do fluido no invólucro, por conta da pressão que exerce, resulta em forças atuando sobre o volume do líquido, representadas por setas na figura.
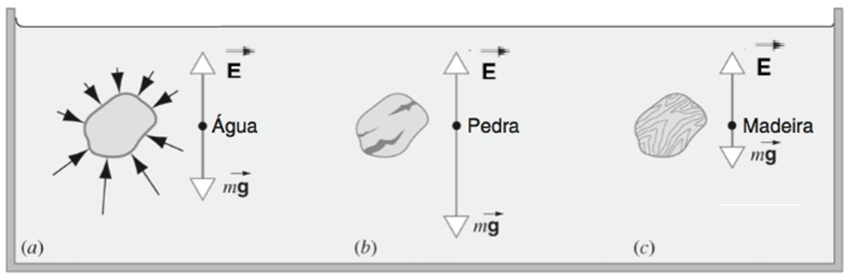
Figura 6: (a) saco plástico com água submerso; (b) pedra submersa; (c) corpo de madeira submerso. Fonte: Adaptada de Halliday; Resnick; Krane (2017).
Na parte inferior do saco com água, é possível ver que as setas direcionadas para cima são maiores do que as setas que apontam para baixo na parte superior. Isso indica que as forças que atuam na superfície inferior do saco com líquido são maiores, o que é resultado do aumento de pressão que ocorre em maiores profundidades. Essa força apontando para cima e que surge sobre corpos imersos é chamada de empuxo (E).
A pressão na superfície de objetos exercida pelo líquido ao seu redor não dependerá do material que constitui o objeto. Sendo assim, se substituíssemos o saco com água por um pedaço de madeira de mesma forma e dimensões idênticas, a força de empuxo não seria alterada. Com isso, podemos concluir que o empuxo ainda seria igual ao peso do volume original do saco com água. Assim, chegamos ao princípio de Arquimedes, que diz que “Um corpo total ou parcialmente imerso em um fluido é sustentado por uma força cuja intensidade é igual ao peso do fluido deslocado pelo corpo” (Halliday; Resnick; Krane, 2017, p. 45).
O princípio de Arquimedes pode ser dado a partir da equação:
$E=\rho_L \cdot V_L \cdot g$
Em que ρL é a massa específica (ou densidade) do líquido, VL é o volume de líquido deslocado, e g é a gravidade no local.
Importante
O volume de fluido deslocado equivale ao volume da porção do objeto que se encontra imersa no líquido.
Corpos densos concentram mais massa por unidade de volume, ou seja, possuem grande massa ocupando um pequeno espaço. Tendo isso em mente, compreenda que, se um objeto submerso na água possui densidade maior que a da água (Figura 6b), o volume de líquido deslocado terá um peso menor que o peso do objeto. Como resultado, o objeto afundará, pois o empuxo será menor que o peso do objeto.
Podemos ir além com essa ideia: se colocássemos uma balança no fundo do recipiente com água e sobre ela o objeto submerso, a balança indicaria a presença de uma força para cima atuando sobre o objeto. Essa força é a resultante das forças atuantes sobre o objeto, dada por P - E (Peso menos Empuxo). É por essa razão que corpos submersos aparentam pesar menos do que pesam fora do líquido.
Curiosidade
Os astronautas se preparam para suas viagens praticando suas tarefas submersos na água contida em grandes reservatórios. Esse procedimento simula as condições de ausência de peso encontradas no espaço (Halliday; Resnick; Krane, 2017).
Se um objeto possui densidade menor que a da água (Figura 6c), ele também ficará sujeito a uma força vertical para cima. No entanto, o peso do objeto será inferior ao peso do fluido deslocado. Isso fará com que o objeto suba até a superfície, de modo que a porção do objeto que permanece submersa possua o volume necessário para deslocar uma quantidade de água com peso equivalente ao peso total do objeto. Neste caso, o corpo flutuará em equilíbrio.
Como é possível, então, saber se um corpo flutua ou afunda? Note as condições para a ocorrência de três situações possíveis dispostas na figura a seguir:
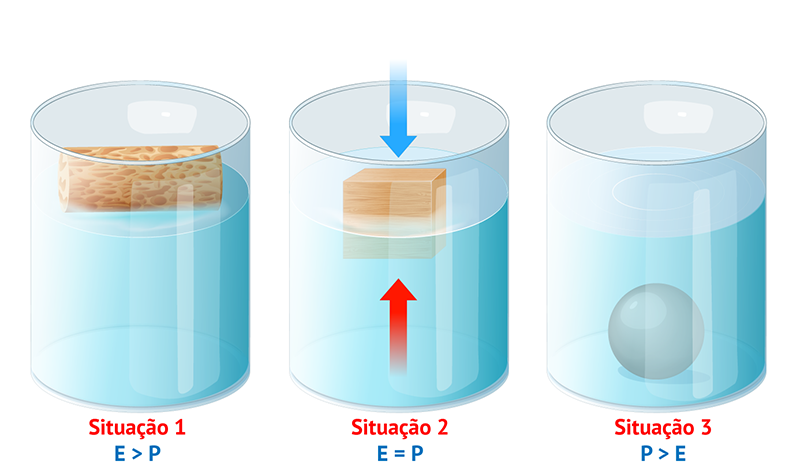
Figura 7: Atuação da força de empuxo em materiais de diferentes densidades. Fonte: Adaptada de Dreamstime.
Agora, teremos uma aplicação da equação de empuxo em um problema.
Por exemplo: um corpo de massa igual a 10 kg foi posto em um reservatório com água até ficar totalmente imerso. Sabendo que a força de empuxo e o peso do corpo estão em equilíbrio, qual seria o volume de água deslocado pelo corpo? Dados: massa específica da água ρL = 1000 kg/m3.
Partiremos da igualdade P = E, já que essas forças estão em equilíbrio:
$\begin{array}{r}P= \\ m \cdot g=\rho \\ m=\rho \\ 10=10\end{array}$
Neste tema, estudamos alguns importantes princípios da hidrostática, como a definição de fluido, substâncias cujas moléculas têm grande mobilidade e, por isso, são capazes de fluir. Fluidos adquirem a forma do recipiente onde são confinados, e percebemos que tanto os líquidos quanto os gases pertencem a essa categoria.
Abordamos que a densidade pode ser entendida como a quantidade de massa contida em um volume, referindo-se a uma característica de um corpo, enquanto a massa específica é uma característica da substância. Estudamos também que a pressão é uma grandeza escalar, fornecida pela razão entre a força e a área onde essa força se aplica.
Por fim, conhecemos o princípio de Arquimedes, que nos garante que um corpo imerso em um fluido está sujeito a uma força vertical, que sempre aponta para cima, chamada de força de empuxo. Vale lembrar que a força de empuxo equivale ao peso do líquido deslocado, sendo uma grandeza vetorial, e, por ser uma força, sua unidade de medida no SI é o newton (N).
Tema 2 - O Princípio de Pascal e o Teorema de Stevin
Neste tema, conheceremos o teorema de Stevin, também conhecido como Lei Fundamental da Hidrostática. Esse importante teorema relaciona a pressão atmosférica com a pressão exercida por um líquido e mostra como a pressão hidrostática varia de acordo com o aumento da profundidade no interior do fluido. Estudaremos como esse estudo contribuiu grandemente para o avanço da hidrostática.
Abordaremos a contribuição do teorema de Stevin na explicação dos vasos comunicantes, onde os fluidos apresentam a mesma altura da coluna de líquido, independente da forma dos recipientes. Esse teorema também contribuiu para o princípio de Pascal, no qual nos aprofundaremos, descobrindo como ele foi responsável pelo avanço no desenvolvimento de dispositivos hidráulicos.
Por fim, estudaremos por que a atuação da pressão exercida pelo ar atmosférico é tão relevante, e definiremos os conceitos de pressão atmosférica, pressão absoluta e pressão manométrica. Encerraremos conhecendo as principais unidades de medida de pressão utilizadas.
O Teorema de Stevin
A aceleração da gravidade atrai os fluidos para a região mais funda dos recipientes, então é coerente pensarmos que a pressão em um líquido é, em sua maior parte, resultado da atuação gravitacional. Analisaremos fluidos em repouso a fim de determinar a pressão em uma profundidade h, medida a partir da superfície do líquido. Para isso, vamos considerar um fluido homogêneo de densidade ρ que se encontra em repouso em um reservatório e supor que pudéssemos visualizar uma parte desse fluido sob a forma de um cilindro, como mostra a Figura 8. Este cilindro se origina na superfície do líquido e vai até a profundidade h. Ele também está em repouso, ou seja, a resultante das forças sobre o cilindro é nula.
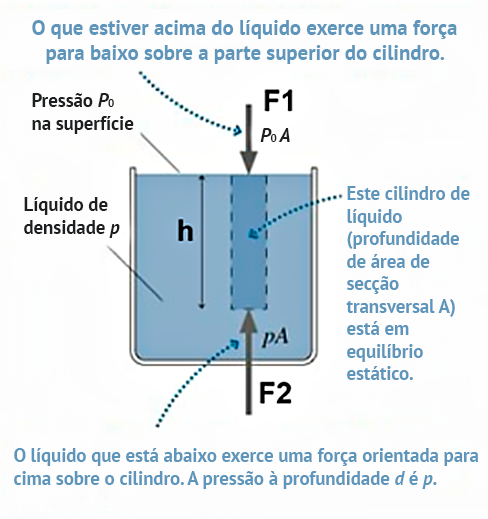
Figura 8: Pressão exercida por uma coluna de líquido. Fonte: Adaptada de Knight (2009).
Em relação às forças atuantes sobre o cilindro de líquido, temos: a força gravitacional ou força peso (m.g) apontando para baixo, a força F1 = P0. A, também orientada para baixo, devida à pressão P0 na superfície do líquido e à força F2 = P. A, orientada para cima, devida à pressão P exercida pelo líquido na parte inferior do cilindro. A pressão P que atua na parte inferior do cilindro é exatamente o que precisamos determinar.
Como a coluna de líquido está em equilíbrio, sabemos que as três forças que atuam sobre ela, quando somadas, têm resultado nulo. Em outras palavras, a força F2 que aponta para cima equilibra a força peso (m.g) e a força F1, que apontam para baixo. Matematicamente, temos:
F2 = F1 + m.g
Da equação da densidade vista no tema anterior, temos que a massa do cilindro é dada por m=ρ.V e o volume 𝑉 V é o produto da área da base 𝐴 A pela altura h, logo: m=ρ.A.h. Voltando à equação das forças sobre o cilindro e fazendo as devidas substituições, temos:
P.A = P0.A + ρ.A.h.g
Como a área A é cancelada em todos os termos, temos como expressão da pressão P na profundidade h:
P = P0 + ρ.h.g
A pressão P dada pela expressão acima é chamada de Pressão Hidrostática, em que ρ é a densidade do líquido.
Importante
A equação da pressão hidrostática parte do pressuposto de que o líquido é incompressível, ou seja, que sua densidade não aumenta com a profundidade.
A equação da pressão hidrostática pode ainda ser escrita da seguinte forma:
P - P0 = ρ.h.g
A diferença de pressão P – P0 é chamada de variação de pressão (∆P).
O que nos leva ao Teorema de Stevin, também conhecido como Lei Fundamental da Hidrostática: “A diferença de pressão entre dois pontos de um fluido em equilíbrio é igual ao produto da massa específica do fluido pela diferença de nível entre os pontos considerados e pela aceleração da gravidade” (Telles; Mongelli Netto, 2013, p.127). Podemos constatar que a pressão hidrostática depende da densidade do fluido, da aceleração da gravidade no local e da profundidade h, além da pressão no nível de referência.
Exemplo
Um mergulhador nada no mar a uma profundidade 100 m. Sabendo que a densidade da água do mar é ρ = 1030 kg/m3 e que a gravidade no local é g = 10 m/s2, calcule a variação de pressão sob a qual o mergulhador se encontra.
Aplicando a equação da pressão hidrostática, temos:
∆P = ρ.h.g
∆P = 1030.100.10
∆P = 19400
∆P = 1,03.106 Pa
O mergulhador está sujeito a uma variação de pressão de 1,03.106 Pa.
A partir da equação da hidrostática, podemos chegar a uma importante conclusão: em um líquido homogêneo e incompressível, a pressão aumenta com a profundidade.
Curiosidade
Como a pressão nas profundezas do oceano é muito grande, as janelas de submersíveis, como submarinos, por exemplo, devem ser muito espessas para suportar grandes forças.
O Teorema de Stevin implica, para fluidos em repouso, que a pressão é a mesma em dois pontos de um líquido que estão em um mesmo nível, ou seja, a mesma profundidade. A Figura 9 ilustra três pontos de um fluido que se encontram no mesmo nível e que, por consequência, estão sujeitos à mesma pressão.
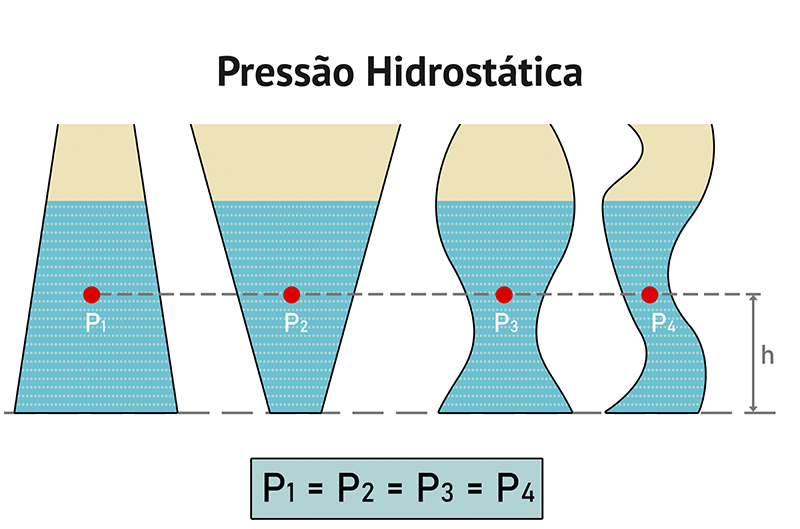
Figura 9: Três pontos distintos com mesma pressão hidrostática. Fonte: Adaptada de Dreamstime.
O Teorema de Stevin se aplica ao caso dos vasos comunicantes, um conjunto de recipientes que são interligados e que podem ter diferentes formatos e tamanhos. Mesmo que, separadamente, cada reservatório tenha uma capacidade própria, ao preencher esses vasos com um fluido, a altura da coluna de líquido será exatamente a mesma para todos os recipientes, como mostra a Figura 10. Podemos explicar esse fenômeno pelo Teorema de Stevin, que conclui que a pressão em um ponto de um fluido independe da forma do recipiente que o contém, mas depende apenas da profundidade do ponto.
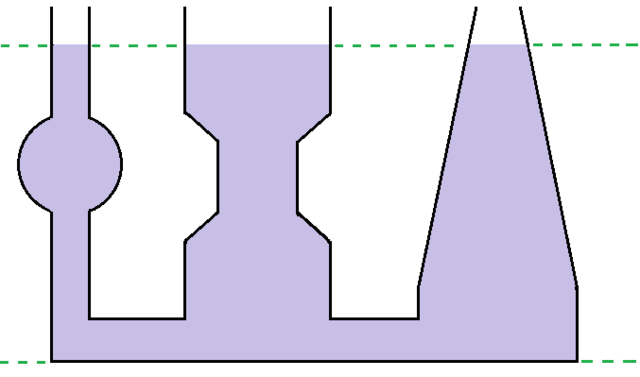
Figura 10: Mesmo nível de líquido em vasos comunicantes. Fonte: Wikimedia Commons.
O Princípio de Pascal
Uma outra consequência do Teorema de Stevin foi o Princípio de Pascal, que afirma que um aumento de pressão exercido em um ponto de um fluido incompressível se transmite integralmente a todos os outros pontos do líquido. O Princípio de Pascal nos permite compreender o funcionamento de diversos dispositivos que utilizam líquidos, geralmente óleos, em seu funcionamento, como elevadores para automóveis, prensas hidráulicas e freios de carros.
Podemos perceber um esquema de uma máquina hidráulica na Figura 11. Essa máquina consiste em um cilindro de área A1 e um pistão móvel, onde se aplica uma força F1. É possível perceber um segundo pistão de área A2, que se comunica com o pistão 1 e sofre atuação de uma força F2.
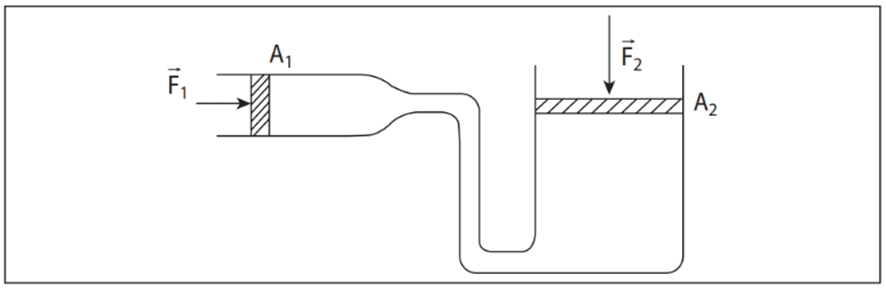
Figura 11: Máquina hidráulica. Fonte: Telles; Mongelli Netto (2013, p.128).
Quando se aplica a força F1, ocorre um aumento de pressão F1/A1 no fluido, que se transmite a todos os pontos do líquido, inclusive à área A2, que fica sujeita a uma pressão F2/A2. Essas pressões se igualam em uma situação de equilíbrio, resultando na equação a seguir:
De forma análoga, funcionam os elevadores hidráulicos, como os utilizados para levantar automóveis em oficinas. Esse dispositivo oferece grande vantagem mecânica, já que multiplica a força aplicada. Para erguer um veículo que exerce uma força peso, resultado de sua massa multiplicada pela gravidade, sobre o pistão 2, é necessário exercer uma força muito menor no pistão 1, conforme ilustra a Figura 12. Em termos mais simples, uma pequena força atuando no pistão menor pode sustentar um automóvel porque tanto a força F1 quanto a F2 exercem a mesma pressão no fluido.
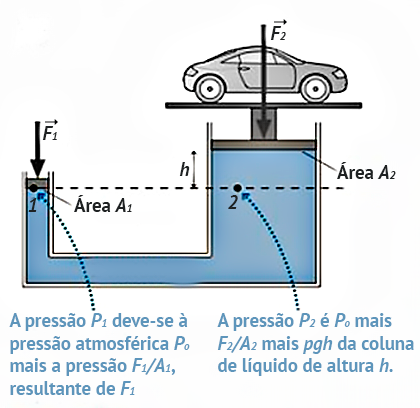
Figura 12: Elevador hidráulico. Fonte: Adaptada de Knight (2009).
Podemos explicar o funcionamento do elevador hidráulico a partir da Terceira Lei de Newton. A força maior F2 empurra o líquido para baixo, e o líquido, por sua vez, empurra o objeto pesado para cima. Teremos, a seguir, um exemplo de aplicação prática do princípio de Pascal.
Exemplo
O elevador hidráulico de uma oficina mecânica utiliza um determinado óleo como fluido hidráulico. Esse dispositivo consiste em um pistão de área 5,0x10-1 m2 e outro de área 0,010m². Qual seria a força necessária, aplicada no pistão menor, para sustentar um veículo 1000 kg colocado sobre o pistão de maior área? Dados: Gravidade g = 10 m/s2.
Compreenda que a força F2 exercida pelo carro é o seu peso (m.g). Apliquemos a equação do princípio de Pascal:
Note que, para equilibrar o automóvel, foi necessário exercer uma força cinco vezes menor que o peso do veículo.
Pressão Manométrica, Barômetros e Unidades de Pressão
A pressão P da equação da hidrostática também é conhecida como pressão absoluta, pois inclui a pressão exercida pelo líquido (pressão hidrostática) e a pressão exercida pela massa de ar acima dele, a pressão atmosférica. Mas seria a pressão do ar, que nem percebemos, tão relevante assim? As dimensões da atmosfera da Terra não se comparam às de um recipiente de laboratório. A imensa altura da atmosfera terrestre é o que torna importante a contribuição gravitacional à pressão, ou seja, o peso da massa de ar está associado a uma grande pressão.
À medida que a altura aumenta, a densidade do ar diminui até que chega a zero nas regiões de vácuo do espaço, o que nos leva à conclusão de que a pressão atmosférica diminui com o aumento da altitude, como mostra a Figura 13.
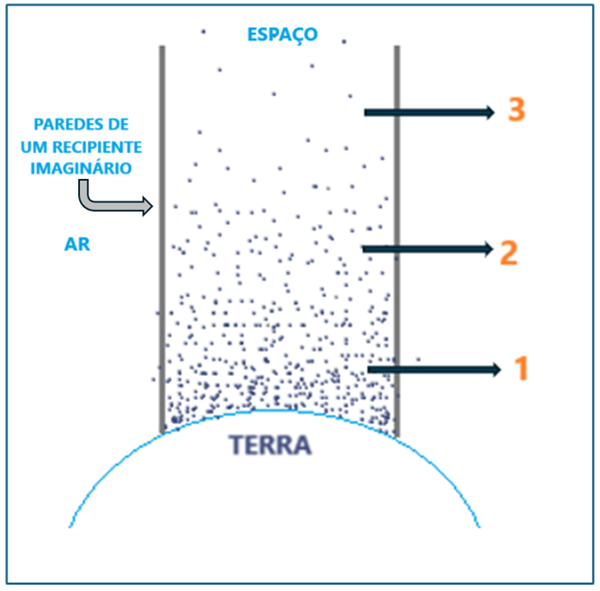
Figura 13: Pressão diminui com o aumento da temperatura. Fonte: Elaborada pela autora.
Na região 1 da Figura 13, percebemos que a pressão e a densidade são maiores próximo à superfície terrestre. Na região 2, a pressão e a densidade diminuem devido à gravidade, até que, na região 3, nas regiões do espaço sideral, pressão e densidade são próximas de zero.
Embora a pressão atmosférica ao nível do mar possa variar de acordo com o clima, a pressão atmosférica média global é aproximadamente 101300P a, então, a atmosfera padrão é definida como 1 atm ≡ 101300 Pa = 101,3 KPa. Por uma questão de simplificação, adotaremos a pressão do ar como ρar = 1 atm. Considere um exemplo simples, mas capaz de mostrar a pressão exercida pelo ar em um cômodo.
Exemplo
Uma sala de aula possui as seguintes dimensões: 5 m de comprimento, 5 m de largura e 3 m de altura. Sabendo que a densidade do ar tem valor próximo de 1,29 kg/m3 e a gravidade no local é 9,8 m/s2, determine:
- a massa e o peso do ar contido na sala;
- a pressão exercida no chão da sala devido ao peso do ar.
O primeiro passo é calcularmos o volume da sala, já que o ar é um gás e ocupará o volume total do cômodo:
V = Largura x comprimento x altura = 5 x 5 x 3 = 75 m3
Agora, basta aplicar a equação da densidade para calcular a massa:
$\begin{gathered}\rho=\frac{m}{v} \\ m=\rho \cdot v \\ =1,29.75 \\ m=96,75 \mathrm{Kg}\end{gathered}$
Por fim, calculamos a pressão no chão de área 5 m x 5 m = 25 m2.
$\begin{gathered}P=\frac{F}{A}=\frac{m \cdot g}{A} \\ \frac{96,75.9,8}{25} \\ \mathrm{P}=37,92 \mathrm{~Pa}\end{gathered}$
A pressão exercida pelo peso do ar no chão é igual a 37,92 Pa.
Medidores de pressão que utilizam a pressão atmosfera como referência são chamados de manômetros, esses dispositivos medem a diferença entre a pressão real e a pressão atmosférica.
Importante
Como a pressão manométrica pode estar acima ou abaixo da pressão atmosférica, seu valor pode ser positivo ou negativo. Entretanto, atenção: a pressão absoluta é sempre positiva!
O barômetro é um aparelho simples e bastante utilizado na medição da pressão. Esse dispositivo consiste apenas em um longo tubo de vidro, com uma extremidade aberta e outra fechada, preenchido com mercúrio. A extremidade aberta é colocada em um recipiente com mercúrio, conforme a Figura 14.
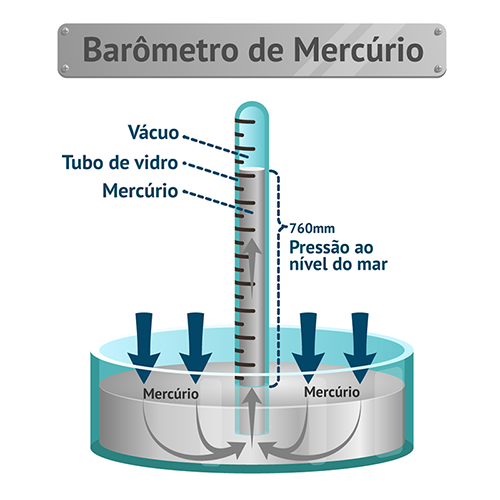
Figura 15: Barômetro de mercúrio. Fonte: Adaptada de Dreamstime.
A parte superior à coluna de mercúrio tem uma pressão tão baixa que pode ser desconsiderada, enquanto a pressão medida sobre a superfície do reservatório de mercúrio é a pressão P que se deseja medir, dada pela equação:
P = ρ.g.h
A conclusão é que, medindo a altura da coluna de mercúrio acima da superfície do recipiente, obtemos a pressão desejada.
Se a superfície do recipiente com mercúrio estiver sujeita à pressão atmosférica (1 atm), utilizando-se o valor padrão para a gravidade, à temperatura de 0oC, então, a altura da coluna de mercúrio é 760 mm. Sendo assim, consideramos que 1 atm = 760 mm de Hg.
Os experimentos com barômetros realizados por Torricelli e Pascal foram os primeiros a mostrar que era possível produzir um vácuo no pequeno volume acima da coluna de mercúrio, como mostra a Figura 14. Isso trouxe avanços para a engenharia, permitindo, no fim do século XVII, a construção da primeira bomba a vácuo.
A pressão pode ser expressa em diferentes unidades de medida, por questões históricas. Ao longo dos anos, diversos cientistas e engenheiros, que trabalhavam com diferentes tipos de fluidos em baixas ou altas pressões, desenvolveram unidades convenientes. Essas unidades são utilizadas até hoje, e é importante que estejamos familiarizados com as conversões entre elas. A Tabela 3 contém as principais conversões básicas de unidades de pressão:
|
Unidade |
Abreviação |
Valor correspondente a 1 atm |
Utilizadas em |
|
Pascal |
Pa |
101,3 KPa |
Unidades do SI: 1 Pa = 1 N/m2 |
|
Atmosfera |
atm |
1 atm |
Geral |
|
Milímetros de mercúrio |
Mm de Hg |
760 mm de Hg |
Pressão barométrica e gases |
|
Polegadas de mercúrio |
Pol |
29,92 polegadas |
Pressão barométrica nas previsões do tempo nos EUA |
|
Libras por polegada quadrada |
Psi |
14,7 Psi |
Engenharia e Indústria |
Tabela 3: Unidades de pressão. Fonte: Knight (2009, p. 34).
Assim, as principais conversões básicas de unidades de pressão envolvem a troca entre diferentes sistemas de medida. A unidade mais comum no Sistema Internacional de Unidades (SI) é o pascal (Pa), mas há outras unidades frequentemente usadas, como o bar, que é igual a 100.000 pascais (ou 10⁵ Pa), e o milibar (mbar), que corresponde a 100 pascais. Essas e as demais conversões são fundamentais em diversas áreas, como a meteorologia, a engenharia e a física, para facilitar a comunicação e garantir a precisão nos cálculos e medições de pressão.
Neste tema, estudamos o Teorema de Stevin e como ele demonstrou que a pressão no interior de um líquido aumenta à medida que a profundidade aumenta. Estudamos que a pressão em um ponto no interior do líquido é resultado da soma da pressão atmosférica com a pressão exercida pelo próprio líquido. Abordamos as principais aplicações do Teorema de Stevin, como os vasos comunicantes, e analisamos o Princípio de Pascal, que demonstra como um aumento de pressão aplicado em um ponto de um fluido é transmitido a todos os outros pontos do fluido.
Finalmente, definimos a pressão atmosférica como a pressão exercida pelo ar, a pressão hidrostática como a pressão exercida por um fluido e a pressão absoluta como a soma de ambas. Também estudamos a pressão manométrica, que é a diferença entre a pressão real e a pressão atmosférica, e analisamos as diferentes unidades de medida de pressão e suas utilizações.
Tema 3 - Equação da Continuidade e Equação de Bernoulli
Neste tema, analisaremos o comportamento de fluidos em movimento, sejam eles gases ou líquidos; iniciaremos, então, um estudo de hidrodinâmica, ou dinâmica dos fluidos. Essa área de estudo é fundamental para a ciência, engenharia e tem aplicação até mesmo em medicina.
Definiremos um conceito de suma importância para tornar mais acessível a complexa análise de fluidos em escoamento: o conceito de fluido ideal. Também analisaremos como a velocidade de escoamento de um fluido varia de acordo com as diferentes áreas das seções transversais de uma tubulação por onde o fluido escoa. A relação entre essas variáveis será dada pela equação da continuidade, que expressa a lei da conservação da massa e nos permite chegar a uma relação matemática capaz de expressar a vazão volumétrica, ou seja, a quantidade de fluido que atravessa uma determinada seção.
Por fim, analisaremos e aplicaremos a equação de Bernoulli, que é baseada na lei da conservação da energia e que também possui vasta aplicação na física e na engenharia, relacionando a velocidade de escoamento com a pressão.
Fluido Ideal e Tipos de Fluxo
Nesta etapa de nossos estudos, analisaremos o movimento dos fluidos. Alguns exemplos de fluidos em movimento são o vento soprando, as corredeiras em uma cachoeira ou até mesmo o petróleo que esguicha em um poço. O movimento de fluidos reais é algo bastante complexo e frequentemente requer técnicas numéricas e computacionais não tão simples para descrever as quantidades relacionadas a esse movimento. Aspectos do movimento dos fluidos, como a turbulência e os redemoinhos, ainda não foram completamente compreendidos; a área da física que estuda esses fenômenos é a Dinâmica dos Fluidos. Esse tema complexo está presente em pesquisas atuais de ciências e engenharia.
Para facilitar nosso estudo, utilizaremos o modelo simplificado de fluido, ou seja, estudaremos apenas o movimento dos fluidos ideais, que podem ser tratados de formas mais simples, mas ainda assim fornecem resultados relevantes e interessantes. Esse modelo simplificado, embora imperfeito, é capaz de fornecer uma boa descrição do escoamento dos fluidos, eliminando detalhes desnecessários, mas captando a essência do fluxo dos fluidos.
Antes de tratar das hipóteses que formulam o modelo de fluido ideal, vamos considerar algumas características gerais do escoamento de um fluido:
-
Escoamento estacionário ou não-estacionário
O escoamento pode ser caracterizado em função dos valores variáveis da pressão, densidade e velocidade de escoamento. Quando essas grandezas variam de forma independente do tempo, temos então um escoamento estacionário. Mesmo que essas variáveis se alterem de um ponto para outro, elas não se alteram com o tempo para um ponto específico. É possível perceber a ocorrência dessa condição em escoamentos a baixas velocidades, como no lento fluxo de um riacho. Já os movimentos não estacionários são percebidos em marés agitadas, onde a velocidade depende do tempo. Existem ainda movimentos turbulentos, como no caso das cascatas, que, além de possuírem uma velocidade de escoamento que varia de forma aleatória entre os instantes de tempo, também variam de um ponto a outro.
-
Escoamento compressível ou incompressível
O escoamento é considerado incompressível quando a densidade do fluido é constante, ou seja, independente das variáveis x, y, z, t. Em geral, os fluidos podem ser considerados incompressíveis. No entanto, até mesmo gases altamente compressíveis podem sofrer variações insignificantes em sua massa específica, permitindo que, para fins práticos, seu escoamento seja considerado incompressível. Isso pode ser observado, por exemplo, em aeronaves voando a velocidades muito inferiores à velocidade do som. Nessa situação, o ar escoando pelas asas do avião é praticamente incompressível.
-
Escoamento viscoso ou não viscoso
Um fluido em movimento possui viscosidade, que é semelhante ao atrito que ocorre no movimento de sólidos. Em outras palavras, a viscosidade age como o atrito cinético, oferecendo resistência ao fluxo. Uma alta viscosidade requer uma força externa maior ou uma pressão maior para que o escoamento se mantenha. A viscosidade depende da temperatura e, sob as mesmas condições, o óleo utilizado em um motor é mais viscoso que a água. Embora não exista escoamento de fluidos sem viscosidade, para fins práticos, os efeitos dela podem ser desconsiderados, permitindo que o escoamento seja analisado como não viscoso.
-
Escoamento Rotacional
Um escoamento é considerado rotacional quando partículas do fluido, que se movem em uma trajetória circular, giram em torno de seu próprio centro de massa. Caso um elemento do fluido percorra uma trajetória circular, mas sem girar em torno de seu centro de massa, o escoamento será chamado de irrotacional.
Agora que definimos alguns princípios básicos, vamos à definição de fluido ideal. Pode-se perceber que o movimento de um fluido ideal é estacionário, não viscoso, incompressível e irrotacional.
A fumaça subindo na Figura 16 começa como um fluxo laminar, em que todos os pontos do fluido possuem a mesma velocidade constante. No entanto, em determinado ponto, ocorre a transição para um fluxo turbulento, caracterizado por mudanças aleatórias na velocidade e formação de vórtices.

Figura 16: Fumaça passando do fluxo laminar para o turbulento. Fonte: Dreamstime.
As águas tranquilas de um rio são um exemplo de fluxo laminar (Figura 17a), enquanto a queda d’água de uma cachoeira (Figura 17c) representa um fluxo turbulento. Como vimos, a fumaça é um exemplo de transição entre o fluxo laminar e o turbulento (Figura 17b).

Figura 17: (a) fluxo laminar; (b) transição entre fluxo laminar turbulento; (c) fluxo turbulento. Fonte: Bauer; Westfall; Dias (2012, p. 44).
Linhas de Corrente e a Equação da Continuidade
Vamos supor que pudéssemos observar um ponto P pertencente a um fluido ideal durante seu escoamento. Como esse movimento é estacionário, a velocidade do ponto não irá variar com o tempo, e toda e qualquer partícula do fluido que passar por P terá uma velocidade idêntica à de P em intensidade, direção e sentido. O vetor velocidade de qualquer ponto do fluido será sempre tangente à linha de corrente. Dessa forma, as partículas do fluido que passam por P seguem a mesma linha contínua, denominada Linha de Corrente.
A Figura 18 ilustra três pontos consecutivos de nosso fluido hipotético:
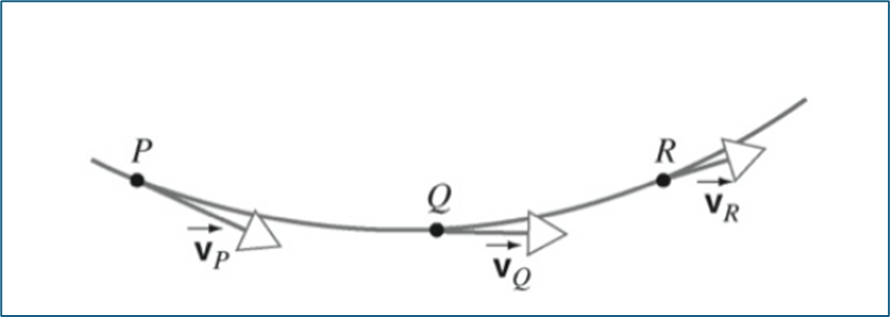
Figura 18: Três pontos P, Q e R pertencentes à mesma linha de corrente. Fonte: Halliday; Resnick; Krane (2017, p. 61).
Uma partícula do fluido que passa por P passará em seguida pelos pontos sucessivos Q e R da linha de corrente. Se uma partícula passou por R, definitivamente, passou por P e Q.
Importante
Duas linhas de corrente não podem se cruzar, pois, caso isso ocorresse, uma partícula em movimento poderia seguir por mais de uma trajetória, e o escoamento não seria estacionário (Halliday; Resnick; Krane, 2017).
A Figura 19 mostra uma interessante aplicação dos conceitos de linhas de corrente. Os engenheiros utilizaram fumaça, caracterizada por um escoamento laminar – percebido pela suavidade e definição do fluxo – para visualizar o fluxo de ar em torno de um veículo colocado em um túnel de vento. As trajetórias não se misturam nem se cruzam; cada trajetória observada é uma linha de corrente do fluido.

Figura 19: Fluxo de ar laminar em torno de um carro em um túnel de vento. Fonte: Knight (2009, p. 41).
Quando se tem um feixe de linhas de corrente vizinhas, essa configuração é chamada de tubo de corrente, como mostra a Figura 20. Vale ressaltar que, como os contornos de um tubo de corrente são formados por linhas de corrente, nenhum fluido pode cruzar os contornos do tubo. Os tubos de corrente são relevantes para nosso estudo, pois se comportam como se fossem uma tubulação com o mesmo formato.
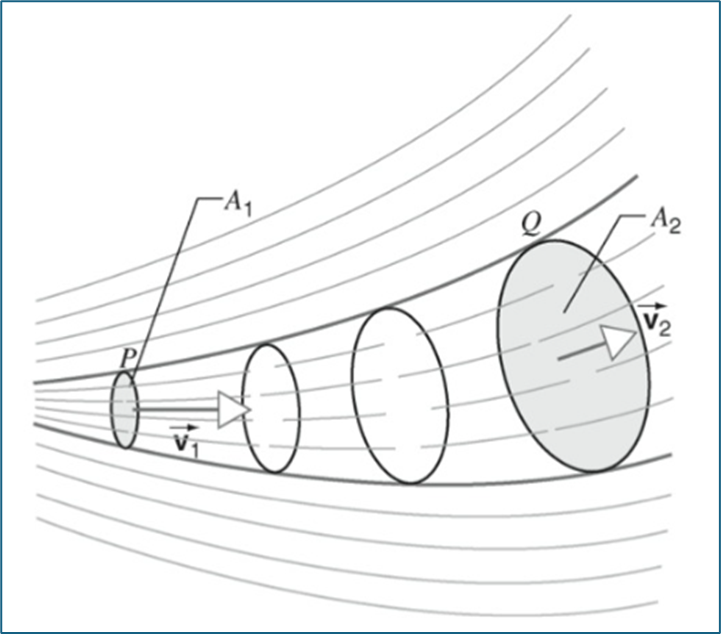
Figura 20: Tubo de corrente. Fonte: Halliday; Resnick; Krane (2017, p. 62).
Como as linhas de corrente nunca se cruzam, os fluidos que entram em P e passam pela área da seção transversal A1 saem em Q e passam pela área A2. Agora, vamos considerar que um fluido ideal se desloque em um tubo de escoamento com áreas de seções transversais diferentes (Figura 20). O fluido escoa inicialmente pela área A1 com velocidade de escoamento v1 e, posteriormente, o fluido escoa pela área A2 com velocidade v2. O volume de líquido que entra na tubulação por unidade de tempo precisa ser igual ao volume de líquido que sai dela, uma vez que o fluido é incompressível.
O volume de líquido por unidade de tempo que passa pela seção A1 pode ser dado por:
$\frac{\Delta V}{\Delta t}=A_1 V_1$
Analogamente, o volume de líquido por unidade de tempo que passa pela seção A2 pode ser dado por:
$\frac{\Delta \mathrm{V}}{\Delta \mathrm{t}}=\mathrm{A}_2 \mathrm{~V}_2$
Como o fluido não pode ser criado nem destruído dentro do tudo e não há vazamentos, o volume de fluido ideal por unidade de tempo que entra no tubo deve se igualar ao volume de fluido ideal por unidade de tempo que sai do tubo. Em termos simplificados, a quantidade de fluido que entra na tubulação deve ser igual à quantidade de fluido que sai da tubulação. E, assim, chegamos à equação da continuidade:
A1.v1 = A2.v2
Em que A1 e A2 são as áreas de seção transversal do tubo, e v1 e v2 são as respectivas velocidades do fluido ao passar por estas áreas. Esse resultado obtido expressa a lei da conservação da massa na dinâmica dos fluidos.
A vazão volumétrica, ou seja, o volume de fluido que passa por uma seção transversal A, é constante e pode ser escrita como:
Q = A.v
Em que v é a velocidade de escoamento do fluido quando passa pela seção A.
O fato de a vazão volumétrica ser constante ao longo de um tubo de corrente implica em uma importante interpretação sobre essas linhas. Na parte mais estreita da tubulação, percebemos as linhas de corrente mais próximas umas das outras (Figura 21), o que indica uma maior velocidade de escoamento do fluido. Em contrapartida, na parte mais larga do tubo, essas linhas estão mais afastadas, indicando que, nessa região, a velocidade do fluido é mais baixa.
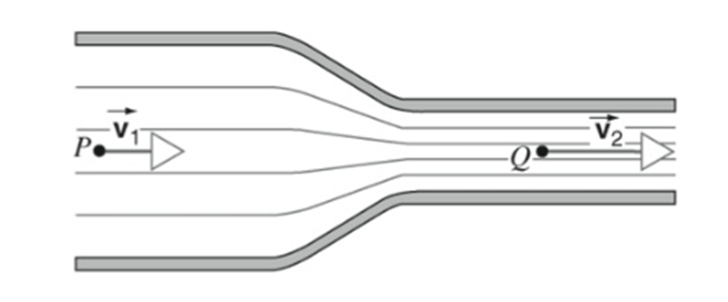
Figura 21: Tubo de escoamento com velocidades de escoamento variando com a seção transversal. Fonte: Halliday; Resnick; Krane (2017, p. 62).
A unidade de medida da vazão Q no sistema internacional é m3/s, mas não é incomum vê-la sendo expressa em cm3/s ou ainda, litros/minutos.
Importante
O fluxo de um fluido é mais rápido em partes mais estreitas de uma tubulação que nas partes mais largas, e isso é uma consequência da equação da continuidade.
Vamos a alguns exemplos.
Exemplo 1: Um certo fluido escoa com velocidade v1 = 4 m/s através de um tubo de área de seção transversal A1 = 20 cm2. Calcule a velocidade com que esse fluido sairá do outro lado do tubo que possui área A2 = 10 cm2.
Aplicaremos a equação da continuidade, dada por:
A1.v1 = A2.v2
Substituindo os valores dados pelo problema, temos:
20.4 = 10.v2
80 = 10.v2
v2 = 80/10
v2 = 8 m/s
O fluido sairá do tubo com velocidade igual a 8 m/s. Observe que, ao passar pela área final do tubo, que é metade da área inicial, a velocidade do fluido dobrou. Assim, confirmamos que a velocidade do fluido aumenta ao passar por áreas mais estreitas.
Exemplo 2: Calcule a vazão volumétrica de petróleo que passa por um oleoduto de área da seção transversal igual a 0,3 m2 com velocidade de 2 m/s.
Sabemos que a vazão volumétrica é dada por:
Q = A.v
Como a área é 0,3 m2 e a velocidade é 2 m/s, temos que
Q = 0,3.2
Q = 0,6 m3/s
A vazão de petróleo no oleoduto é 0,6 m3/s.
A Equação de Bernoulli
Quando um fluido ideal escoa em um tubo, suas condições podem ser alteradas pela variação na área da seção transversal do tubo. No entanto, essas condições também podem se modificar se a entrada e a saída da tubulação estiverem em níveis diferentes ou se houver diferença na pressão de entrada e saída. Sabemos que a equação da continuidade relaciona as velocidades de escoamento do fluido com a variação na área da seção transversal. Contudo, será necessário utilizar uma equação que relacione as variações de área, pressão e níveis na tubulação, já que diferenças de pressão e de nível podem acelerar um elemento do fluido.
Sendo assim, aplicaremos a lei da conservação de energia a um fluido ideal que escoa em um tubo com diferença de nível, como mostra a Figura 22.
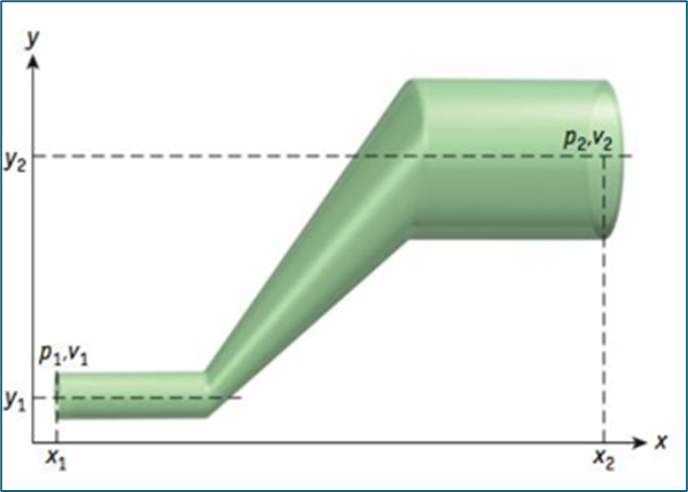
Figura 22: Fluido ideal escoamento em um tubo com diferentes níveis. Fonte: Bauer; Westfall; Dias (2012, p. 45).
Vamos considerar que, na parte mais baixa do tubo, o fluido, que tem densidade constante ρ, possui pressão P1, velocidade V1 e altura Y1. Quando esse fluido escoa para a parte mais alta, será caracterizado por uma pressão P2, velocidade V2 e altura Y2. A equação de Bernoulli relaciona as diferentes pressões e velocidades da seguinte forma:
$p_1+\frac{1}{2} \rho v_1^2+\rho g y_1=p_2+\frac{1}{2} \rho v_2^2+\rho g y_2$
Ou, ainda, para o caso de o escoamento ser estacionário, incompressível, sem viscosidade e irrotacional, a equação de Bernoulli pode ser escrita como:
$p+\frac{1}{2} \rho v^2+\rho g y=$ constante
Importante
Se o fluido escoa em um tubo com Y=0, ou seja, elevação constante, a consequência será que
$P+\frac{1}{2} \rho \cdot v^2=$ constante
Então, se a velocidade do fluido aumenta, a pressão tem que diminuir.
Exemplo 3 (Adaptado de Knight, 2009, p. 44):
Considere a água que está fluindo pelos canos mostrados na Figura 8 um fluido ideal e que obedece à equação de Bernoulli. A velocidade do fluido pelo cano mais baixo é de 5,0 m/s, e um manômetro marca a pressão de 75 KPa. Qual é a leitura do manômetro no cano superior, onde o fluido passa com velocidade V2 = 12 m/s?
Dados: g = 9,8 m/s2 e ρágua = 1000 kg/m3.
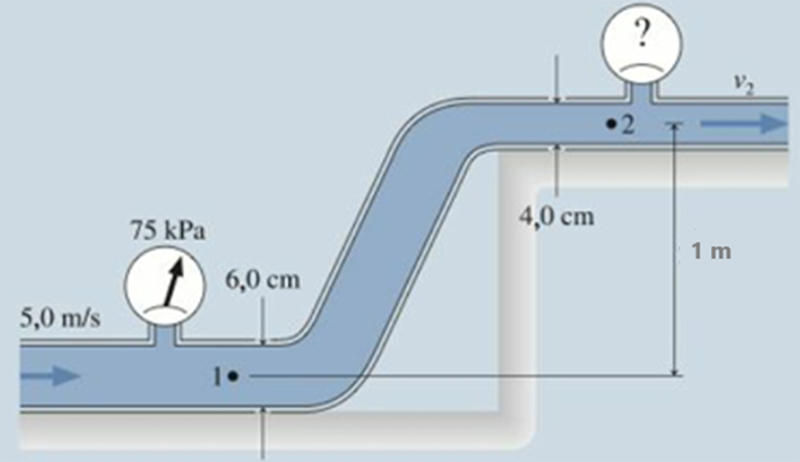
Figura 23: Água fluindo em uma tubulação. Fonte: Adaptada de Knight (2009).
Como o problema informou que o ponto 1 está na parte mais baixa do tubo, consideremos esse ponto como o nível de referência (Y1 = 0), aplicaremos a equação de Bernoulli e substituiremos os valores do enunciado:
87500 = P2 + 72000 + 980
P2 = 87500 – 72980
P2 = 14500
P2 = 14,5 KPa
Em comparação ao ponto mais baixo, a água passa pelo ponto mais alto da tubulação com velocidade maior e pressão menor no valor aproximado de 14,5 Kpa.
Neste tema, estudamos as hipóteses que formulam o modelo de fluido ideal e definimos esse tipo de fluido quanto ao seu escoamento, que deve ser estacionário, não viscoso, incompressível e irrotacional. Também analisamos que os tipos de fluxo dependem da velocidade e da viscosidade do fluido, sendo classificados como laminar, turbulento ou de transição entre o laminar e o turbulento.
Definimos os conceitos de linha de corrente e de tubo de corrente, que, para fins de estudo, é análogo a uma tubulação real. Analisamos a equação da continuidade, que determina que o volume de fluido que entra por uma seção da tubulação deve ser igual ao volume que sai por outra seção do tubo. Essa relação reflete a lei da conservação da massa, uma vez que o fluido não é criado nem destruído no interior dos tubos. Observamos, ainda, uma importante consequência da equação da continuidade: o fluxo possui maior velocidade ao passar por regiões mais estreitas e menor velocidade ao passar por seções mais largas.
Por fim, exploramos a equação de Bernoulli, que relaciona as pressões e velocidades de um fluido que escoa por uma tubulação com diferença de níveis, levando-nos à conclusão de que, se a velocidade de escoamento do fluido aumentar, a pressão diminuirá.
Além da Sala de Aula
Na leitura indicada, o autor aborda a equação de Bernoulli, uma relação entre as velocidades e pressões de um fluido escoando por uma tubulação com diferentes alturas, além da equação da continuidade. O texto também demonstra fenômenos bastante interessantes que podem ser explicados com base nas conclusões derivadas dessas equações.
O autor explica como o efeito Bernoulli, caracterizado pelo aumento de velocidade decorrente de uma diminuição de pressão, pode ser percebido em eventos cotidianos e, ao mesmo tempo, explicar fenômenos mais complexos, como a sustentação de uma aeronave em pleno voo. Por fim, trata de um aparelho desenvolvido a partir da equação da continuidade e da equação de Bernoulli, chamado tubo de Venturi, utilizado para criar uma diferença de pressão que pode ser empregada no acionamento de instrumentos de navegação.
Todos esses pontos são tratados por Bauer, Westfall e Dias (2012), por isso, faça a leitura da página 46 à 51 do livro Física para universitários, disponível na Minha Biblioteca.
Lembre-se de que, para iniciar a leitura do livro sinalizado, é necessário fazer login na Minha Biblioteca.
Título do livro/artigo: Física para universitários
Páginas indicadas: 46 a 51
Referência: BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: AMGH, 2012.
Na leitura indicada, o autor aborda o importante Teorema de Arquimedes e a lei do empuxo, estabelecendo uma relação entre esses conceitos e o fato de alguns corpos boiarem enquanto outros afundam quando imersos em um líquido. Em seguida, o autor elucida o motivo pelo qual os navios não afundam, mesmo quando agitados pelas ondas.
O autor também explica procedimentos estáticos para a medição de pressão em fluidos, apresentando instrumentos e diferentes unidades de medida dessa grandeza, além de problemas resolvidos sobre o tema. Por fim, o conceito de tensão superficial é abordado, desvendando o motivo pelo qual folhas e até mesmo insetos podem pairar sobre a superfície da água sem afundar.
Todos esses pontos são tratados por Halliday, Resnick e Krane (2017), por isso, faça a leitura da página 45 à 50 do livro Física 2, disponível na Minha Biblioteca.
Lembre-se de que, para iniciar a leitura do livro sinalizado, é necessário fazer login na Minha Biblioteca.
Título do livro/artigo: Física 2
Páginas indicadas: 45 a 50
Referência: HALLIDAY, D.; RESNICK, R.; KRANE, K. S. Física. 5. ed. Rio de Janeiro: LTC, 2017. v. 2.
A Física nas Embarcações
Neste estudo de caso, analisaremos as razões pelas quais os navios, mesmo possuindo grande massa e dimensões enormes, são capazes de flutuar. Abordaremos como, com todo o peso que possuem, conseguem permanecer na superfície da água e não afundam diretamente. Também exploraremos como a densidade da água e a densidade média da embarcação são fatores determinantes, assim como o equilíbrio das forças atuantes, para que este fenômeno ocorra.
Considere a seguinte situação: a física hidrostática possui vasta aplicação no ramo da engenharia, especialmente nas construções de embarcações. Para compreender a estabilidade de uma embarcação, é necessário dominar os conceitos de centro de gravidade, densidade, pressão hidrostática e empuxo. O papel da hidrostática é definir o comportamento do corpo flutuante, que resulta da interação entre o peso da embarcação e as forças oriundas da água.
Os navios são exemplos de embarcações de grande porte, produzidas em madeira, ferro ou aço, e costumam ter massas de centenas de toneladas. É bastante curioso que um corpo tão "pesado" não afunde. O navio é projetado de modo que possa retornar à sua posição inicial em caso de oscilações. Isso ocorre porque seu centro de gravidade fica abaixo do centro de empuxo, gerando uma situação de equilíbrio estável. Entretanto, outros fatores também contribuem para a estabilidade de um navio.
Sabemos que a flutuação de um objeto depende de sua densidade, da densidade do líquido e do empuxo. No caso de um navio, apesar de sua grande massa, ele possui também um grande volume, o que resulta em uma densidade média menor. Além disso, o navio é capaz de deslocar um grande volume de água, contribuindo para sua flutuação.

Questionamentos para reflexão:
- Quando o navio desloca um volume de água, a água exerce alguma força sobre o navio? Por que os navios possuem uma parte oca?
- Se os navios têm grande massa e, consequentemente, grande peso, por que não afundam?
- Se uma parte da estrutura do navio se romper, de modo que comece a entrar água, por que o navio afundaria?
Assista às videoaulas a seguir, que têm como objetivo reforçar os conteúdos abordados nesta unidade de maneira didática para embasar os conceitos e teorias trabalhados. Esperamos que contribuam significativamente para seu aprendizado e que a busca pelo conhecimento não se encerre neste percurso de aprendizagem.
Neste infográfico, trataremos dos princípios fundamentais da hidrostática, o ramo da física que analisa o comportamento de fluidos em repouso a partir das variáveis pressão e densidade. Esta área de estudo é responsável por examinar a atuação das forças sobre corpos imersos em fluidos, que podem ser tanto líquidos quanto gases. Embora líquidos e gases sejam fluidos, eles apresentam diferenças importantes.

Nesta unidade, estudamos o que são fluidos e como estes podem ser líquidos ou gases. Verificamos que a densidade é um dos fatores que influenciam na flutuabilidade de um corpo quando colocado em um líquido. Analisamos, pelo Teorema de Arquimedes, que todo corpo imerso em um fluido sofre a atuação da força de empuxo.
Definimos pressão como força por unidade de área e a pressão absoluta em um ponto de um líquido como a soma entre a pressão hidrostática e a pressão atmosférica. Observamos que a pressão aumenta com a profundidade, mas que o Teorema de Stevin garante que, para fluidos em repouso, a pressão é a mesma em dois pontos que estejam no mesmo nível.
Conhecemos o modelo de fluido ideal, utilizado em nosso estudo de fluidos em movimento, e estudamos que a equação da continuidade é uma expressão matemática que relaciona a velocidade de escoamento de um fluido com a área disponível para que ele flua. Finalmente, conhecemos a equação de Bernoulli, que nos mostra como a velocidade de um fluido escoando em um tubo varia quando a pressão aumenta ou diminui.
Para sua autorreflexão:
- Analisou, a partir do teorema de Arquimedes, quais objetos flutuam ou afundam na água?
- Assimilou como o Teorema de Stevin se aplica às situações práticas a ponto de conseguir calcular a pressão total em um corpo totalmente submerso?
- Aplicou a equação de Bernoulli em uma situação real e conseguiu calcular a velocidade de escoamento?
BAUER, W.; WESTFALL, G. D.; DIAS, H. Física para universitários. Porto Alegre: AMGH, 2012.
HALLIDAY, D.; RESNICK, R.; KRANE, K. S. Física. 5. ed. Rio de Janeiro: LTC, 2017. v. 2.
KNIGHT, R. D. Física uma abordagem estratégica: termodinâmica óptica. 2. ed. Porto Alegre: Bookman, 2009. v. 2.
PLETSCH, M. Vasos comunicantes. Laboratório de Ensino de Física, UFRGS, 2024. Disponível em: https://www.ufrgs.br/labensif/wp-content/uploads/tainacan-items/6563/7699/vasos-comunicantes.pdf. Acesso em:19 out. 2024.
TELLES, D. D.; MONGELLI NETTO, J. Física com aplicação tecnológica. 2. ed. São Paulo: Blücher, 2013.







